函数
function [x,y]=euler(f,xinit,yinit,xfinal,n)
h=(xfinal-xinit)/n
x=[xinit zeros(1,n)];
y=[yinit zeros(1,n)];
for i=1:n
x(i+1)=x(i)+h;
y(i+1)=y(i)+h*f(x(i),y(i));
end
end
matlab代码
f=@(x,y)-50*y+50*x^2+2*x
g=@(x)1/3*exp(1).^(-50*x)+x.^2
xe=[0:0.05:1]
ye=g(xe)
[x1,y1]=euler(f,0,1/3,1,20)
plot(xe,ye,'-',x1,y1,'r-')
xlabel('x')
ylabel('y')
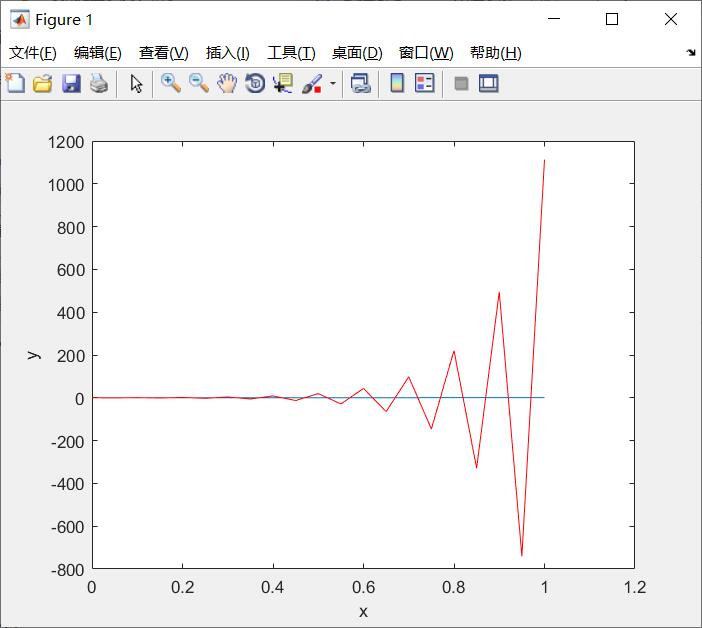
结果如图,当[x1,y1]=euler(f,0,1/3,1,20)时,函数值很大,求解错误。
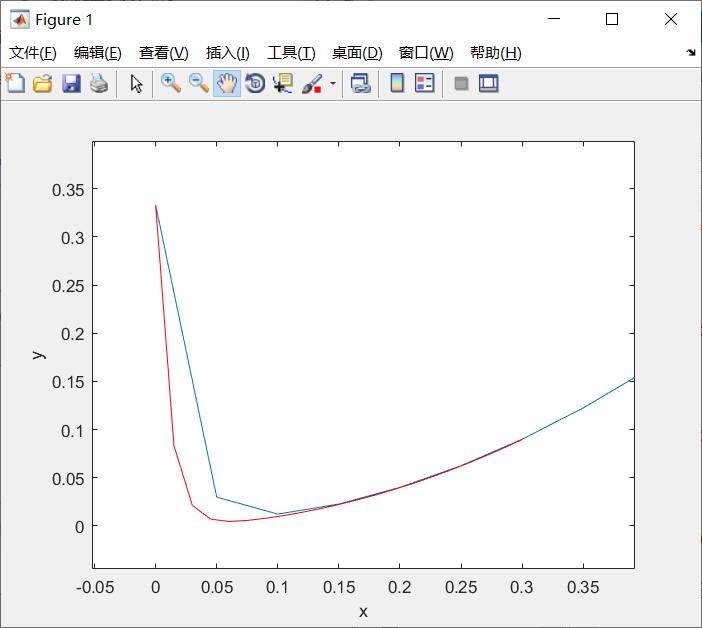
当[x1,y1]=euler(f,0,1/3,0.3,20)时,近似正确
问题原题:
y'=-50y+50x^2+2x
y(0)=1/3
0≤x≤1
请问大佬问题出在哪里,应该怎么改呢?
