1.在使用ode45的时候,方程式fun是通过一系列运算得到的,fun用变量字母代入后,没法把初始值带入其中
2,代码如下
```clear all
clc
syms t u(t) x(t) a b
%Af1=basicF3(1,10,u); %Af1为状态函数1的基函数
Af1=basicF3(x(1),x(2),u); %Af1为状态函数1的基函数
n1=size(Af1,2); %n1为基函数的维度:列数
A1=rand(n1,1); %随机生成A1
Af2=Af1; %Af2为状态函数1的基函数
A2=rand(n1,1); %随机生成A2
A=[A1', A2']'; %A:状态方程的系数矩阵
Af=[Af1,Af2]; %Af:多项式基函数
AF=[Af1 zeros(1,size(Af2,2));zeros(1,size(Af1,2)) Af2]; %f:状态方程的多项式基函数
%Bf=basicF2(1,10); %Bf为控制函数的基函数
Bf=basicF2(x(1),x(2)); %Bf为控制函数的基函数
n2=size(Bf,2); %n2为基函数的维度:列数
B=rand(n2,1); %B为控制函数u的系数矩阵
%BF=diag(Bf) %f:状态方程的多项式基函数
BF=Bf; %参考AF
U=sum(BF*B); %控制策略方程
%Afu1=basicF3(1,10,U) ;
Afu1=basicF3(x(1),x(2),U) ; %Af1为状态函数的基函数(代入u)
Afu2=Afu1;
AFU=[Afu1 zeros(1,size(Afu2,2));zeros(1,size(Afu1,2)) Afu2] ;
y=AFU*A;
dx=zeros(2,1)
dx(1)=sum(y.*[1;0])
dx(2)=sum(y.*[0;1])
tspan = [0,15];
x0 = [0;1];
[t, x] = ode45(@dx, tspan, x0);
3

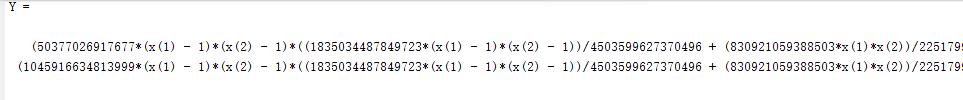
4.自己检测后发现
Y没法根据x(1) x(2)改变而改变 就是x(1) x(2)赋值之后没变法代入到Y里面 所以ode45里面就没把初始值带进去 出现了类型问题 dx带不进去数
有大佬遇到过这种问题吗,跪求看看
