指定有向带权图中的任意几点，如何求出是否存在通路以及通路的最短路径？

Question

指定有向带权图中的任意几点，如何求出是否存在通路以及通路的最短路径？

Answer 1

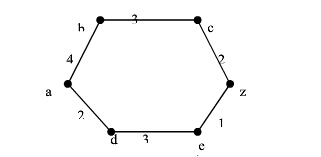
虽然这是一个无向的，但是主要还是方法。
面对这个问题主要还是先解决起点（设为a）到其他点的最短通路，直到找到你所指定的一点（设为z）
w(a,b)=4 w(a,d)=2 w(b,c)=3 w(d,e)=3 w(e.z)=1 w(c,z)=2

1、初始P={a},T={b,c,d,e,z} D(b)=4;D(c)=∞；D(d)=2;D(e)=∞；D(z)=∞；其中p表示求得最小距离的顶点集合，其中D(a)=0

            由此可以看出D(d)=2是距离a最近的，将它放到P集合中
            2、P={a,d},T={b,c,e,z}
                    D(x)=min{上一步计算的D(x),上一步新加到P集合的点到x的距离+新加的最短距离}
                    所以：
                    D(b)=min{4, ∞}=4;
                    D(c)=min{∞，∞}=∞；
                    D(e)=min{∞，2+3}=5；
                    D(z)=min{∞.∞}=∞;
                    由此可知D(b)是最小的，
            3、P={a,d,b},T={c,e,z}
                    D(c)=min{∞,D(b)+w(b,c)}=7;
                    D(e)=min{5,∞}=5;
                    D(z)=min{∞,∞}=∞;
                    将e放到P中依次类推，知道找到你选定的终点为止。