利用matlab解决这个格式,他的初值条件为在一个区间内,给定一个值。[A,B]区间,a,b为初值。利用matlab做出这个格式。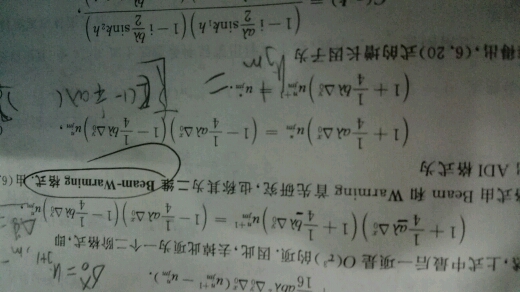
解决二维双曲型方程beam-warming格式
- 写回答
- 好问题 0 提建议
- 追加酬金
- 关注问题
- 邀请回答
-
1条回答 默认 最新
悬赏问题
- ¥88 找成都本地经验丰富懂小程序开发的技术大咖
- ¥15 如何处理复杂数据表格的除法运算
- ¥15 如何用stc8h1k08的片子做485数据透传的功能?(关键词-串口)
- ¥15 有兄弟姐妹会用word插图功能制作类似citespace的图片吗?
- ¥200 uniapp长期运行卡死问题解决
- ¥15 请教:如何用postman调用本地虚拟机区块链接上的合约?
- ¥15 为什么使用javacv转封装rtsp为rtmp时出现如下问题:[h264 @ 000000004faf7500]no frame?
- ¥15 乘性高斯噪声在深度学习网络中的应用
- ¥15 关于docker部署flink集成hadoop的yarn,请教个问题 flink启动yarn-session.sh连不上hadoop,这个整了好几天一直不行,求帮忙看一下怎么解决
- ¥15 深度学习根据CNN网络模型,搭建BP模型并训练MNIST数据集
