#include
#include
#include
typedef int Status;
#define OK 1;
#define ERROR 0;
typedef struct BiTNode
{
char data; //数据域;Type: 用户定义数据类型
struct BiTNode *Lchild; //左指针域
struct BiTNode *Rchild; //右指针域
} BiTNode, *BiTree;
Status IniBiTree(BiTree &T)
{
//构造空树
T = (BiTNode *)malloc(sizeof(BiTNode));
if (!T)return ERROR;//构造失败
T->Lchild = T->Rchild = NULL;
return OK;
}
void CreateBiTree(BiTree &T)
{
//按先序次序输入二叉树中结点的值(一个字符),#字符表示空数,
//构造二叉链表表示的二叉树T。
char ch;
scanf_s("%c",&ch,2);
if (ch == '#')T = NULL;
if (ch == '0')return;
else
{
T = (BiTNode *)malloc(sizeof(BiTNode));
if (!T) exit(OVERFLOW);//分配失败
T->data = ch;
CreateBiTree(T->Lchild);//构造左子树
CreateBiTree(T->Rchild);//构造右子树
}
}//CreateBiTree
Status IsEmpty(BiTree T)
{
if (T)return ERROR;//非空树
return OK;//空树
}
void ClearBiTree(BiTree &T)
{
if (T)
{
if(T->Lchild)
ClearBiTree(T->Lchild);//如果有左孩子
if (T->Rchild)//如果有右孩子
ClearBiTree(T->Rchild);
free(T);//释放结点
T = NULL;//根节点为空
}
}
char GetRoot(BiTree T)
{
if (!T) return 'E';//如果是空树
else return T->data;
}
int GetDepth(BiTree T)
{//求的树的深度
int i,j;//i,j分别用来记左子树和右子树
if (!T) return 0;
if (T->Lchild) i = GetDepth(T->Lchild);
else i=0;
if (T->Rchild) j = GetDepth(T->Rchild);
else j=0;
return i > j ? i + 1 : j + 1;
}
void PreOrderTraverse(BiTree T)
{//采用二叉链表存储结构
//先序遍历二叉树T的递归算法。
if (T == NULL)return;
printf("%c", T->data);
PreOrderTraverse(T->Lchild);//遍历左子树
PreOrderTraverse(T->Rchild);//遍历右子树
}//PreOrderTraverse
void InOrderTraverse(BiTree T)
{//采用二叉链表存储结构
//中序遍历二叉树T的递归算法。
if (T == NULL)return;
InOrderTraverse(T->Lchild);//遍历左子树
printf("%c", T->data);
InOrderTraverse(T->Rchild);//遍历右子树
}//InOrderTraverse
void PostOrderTraverse(BiTree T)
{//采用二叉链表存储结构
//后序遍历二叉树T的递归算法。
if (T == NULL)return;
printf("%c", T->data);
PostOrderTraverse(T->Lchild);//遍历左子树
PostOrderTraverse(T->Rchild);//遍历右子树
}//PostOrderTraverse
int main()
{
BiTree tree;
IniBiTree(tree);//初始化二叉树
CreateBiTree(tree);//创建二叉树
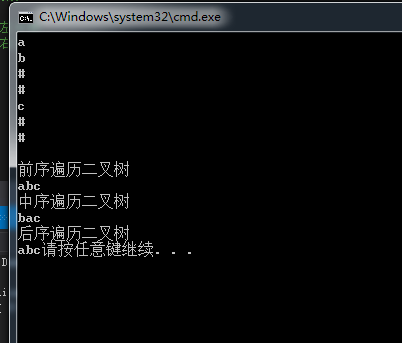
printf("\n前序遍历二叉树\n");
PreOrderTraverse(tree);//前序遍历二叉树
printf("\n中序遍历二叉树\n");
InOrderTraverse(tree);//中序遍历二叉树
printf("\n后序遍历二叉树\n");
PostOrderTraverse(tree);//后序遍历二叉树
system("pause");
return 0;
}