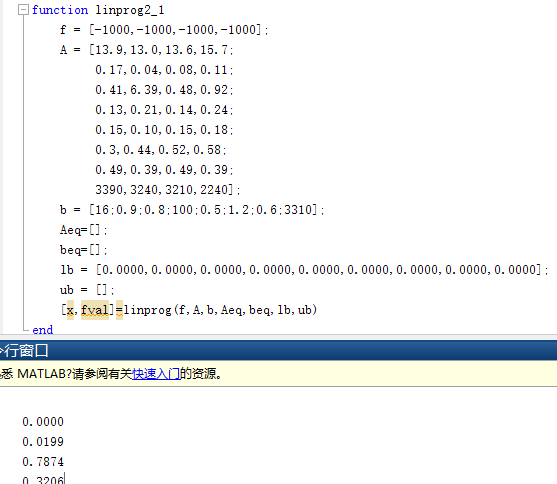
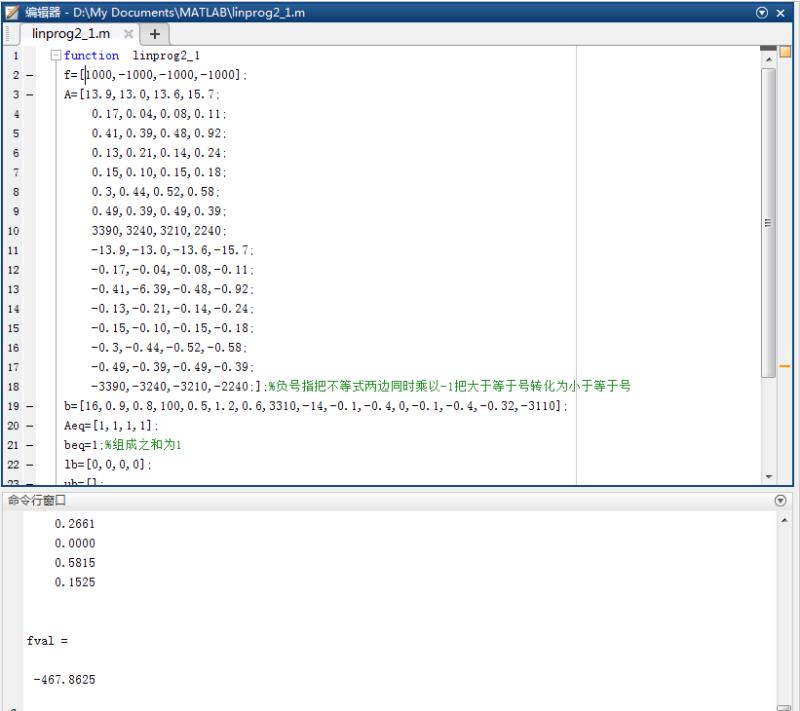
单价都是1000,X1到X4是4中原料占比,总和为100%,求解成本最低的最优解
答案(X1=26.26%,X2=0.00%,X3=58.15%,X4=15.25%)
Min s = 1000 * X1 + 1000 * X2 + 1000 * X3 + 1000 * X4;
14<= 13.9 * X1 + 13.0 * X2 + 13.6 * X3 + 15.7 * X4 <=16;
0.1<= 0.17 * X1 + 0.04 * X2 + 0.08 * X3 + 0.11 * X4 <= 0.9
0.4<= 0.41 * X1 + 0.39 * X2 + 0.48 * X3 + 0.92 * X4 <=0.8;
0<=0.13 * X1 + 0.21 * X2 + 0.14 * X3 + 0.24 * X4 <= 100;
0.1<=0.15 * X1 + 0.10 * X2 + 0.15 * X3 + 0.18 * X4 <= 0.5;
0.4<=0.3 * X1 + 0.44 * X2 + 0.52 * X3 + 0.58 * X4 <= 1.2;
0.32<=0.49 * X1 + 0.39 * X2 + 0.49 * X3 + 0.39 * X4 <=0.6;
3110<=3390 * X1 + 3240 * X2 + 3210 * X3 + 2240 * X4 =3310;