Problem Description
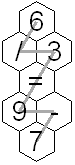

An amusing puzzle consists of a collection of hexagonal tiles packed together with each tile showing a digit or '=' or an arithmetic operation '+', '-', '*', or '/'. Consider continuous paths going through each tile exactly once,
with each successive tile being an immediate neighbor of the previous tile. The object is to choose such a path so the sequence of characters on the tiles makes an acceptable equation, according to the restrictions listed below. A sequence is illustrated in each figure above. In Figure 1, if you follow the gray path from the top, the character sequence is"6/3=9-7". Similarly, in Figure 2, start from the bottom left 3 to get "3*21+10=73".
There are a lot of potential paths through a moderate sized hex tile pattern. A puzzle player may get frustrated and want to see the answer. Your task is to automate the solution. The arrangement of hex tiles and choices of characters in each puzzle satisfy these rules:
The hex pattern has an odd number of rows greater than 2. The odd numbered rows will all contain the same number of tiles. Even numbered rows will have one more hex tile than the odd numbered rows and these longer even numbered rows will stick out both to the left and the right of the odd numbered rows.
1.There is exactly one
2. '=' in the hex pattern.
3. There are no more than two '*' characters in the hex pattern.
4. There will be fewer than 14 total tiles in the hex pattern.
5.With the restrictions on allowed character sequences described below, there will be a unique acceptable solution in the hex pattern.
To have an acceptable solution from the characters in some path, the expressions on each side of the equal sign must be in acceptable form and evaluate to the same numeric value. The following rules define acceptable form of the expressions on each side of the equal sign and the method of expression evaluation:
6.The operators '+', '-', '*', and '/' are only considered as binary operators, so no character sequences where '+' or '-' would be a unary operator are acceptable. For example "-2*3=-6" and "1 =5+-4" are not acceptable.
7.The usual precedence of operations is not used. Instead all operations have equal precedence and operations are carried out from left to right. For example "44-4/2=2+3*4" is acceptable and "14=2+3*4" is not acceptable.
8.If a division operation is included, the equation can only be acceptable if the division operation works out to an exact integer result.
For example "10/5=12/6" and "7+3/5=3*4/6" are acceptable. "5/2*4=10"
is not acceptable because the sides would only be equal with exact mathematical calculation including an intermediate fractional result. "5/2*4=8" is not acceptable because the sides of the equation would
only be equal if division were done with truncation.
9.At most two digits together are acceptable. For example, " 9. 123+1 = 124" is not acceptable.
10.A character sequences with a '0' directly followed by another digit is not acceptable. For example,"3*05=15" is not acceptable.
With the assumptions above, an acceptable expression will never involve an intermediate or final arithmetic result with magnitude over three million.
Input
The input will consist of one to fifteen data sets, followed by a line containing only 0. The first line of a dataset contains blank separated integers r c, where r is the number of rows in the hex pattern and c is the number of entries in the odd numbered rows. The next r lines contain the characters on the hex tiles, one row per line. All hex tile characters for a row are blank separated. The lines for odd numbered rows also start with a blank, to better simulate the way the hexagons fit together. Properties 1-5 apply.
Output
There is one line of output for each data set. It is the unique acceptable equation according to rules 6-10 above. The line includes no spaces.
Sample Input
5 1
6
/ 3
=
9 -
7
3 3
1 + 1
- 2 0 = 3 3 7 5 2 9 -
- 2 = 3 4
- 8 3 4 / 0
Sample Output
6/3=9-7
3*21+10=73
8/4+3*9-2=43
