Description
One year and a half after owning his first art gallery, RoBa has recently built his second art gallery. Just like before, in order to protect his cherished artworks from theft, he has hired security guards. In addition, He wants to install one or two surveillance cameras so that he can watch by himself day and night everything happening inside the gallery.
RoBa is reusing his plan of camera monitoring which has proved working with his first gallery. The gallery has a nice shape of a convex polygon. (Different from that of his first gallery, this polygon may not have cocircular vertices.) Tall and opaque walls stand on the edges of the polygon. A camera can be installed anywhere inside the gallery hanging from the ceiling or on the walls. A single camera’s sight is an infinite wedge emanating from the place the camera is installed and not blocked by any walls. The cameras are fixed. Once installed, they cannot move or rotate themselves.
The cost of having a camera installed is proportional to the angle spanned by the wedge the camera covers. RoBa wants to minimize the cost of his monitoring plan. Given the shape of the gallery, how should the camera(s) be installed?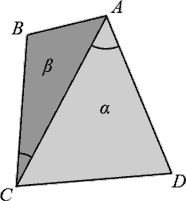
In the illustration to the left (not describing the sample test case), two cameras should be installed at points A and C covering wedges α and β respectively. The cost can be measured by the sum of ∠CAD and ∠ACB.
Input
The input consists of a single test case. The first line contains an integer n (3 ≤ n ≤ 100), indicating that he polygon has n vertices. Each of the next n lines contains a pair of real numbers xi, yi, the coordinates of the i-th vertex. The vertices are listed in counterclockwise order. Any three of them are not collinear.
Output
Output the sum of angles spanned by the camera(s) in radians. A special checker program that admits an absolute error of 10−6 is used to verify your answer.
Sample Input
4
0 0
1 0
1 1
0 1
Sample Output
1.5707963267949
