我把问题再详细讲述一下,图是无向多重图,如下图所示的图 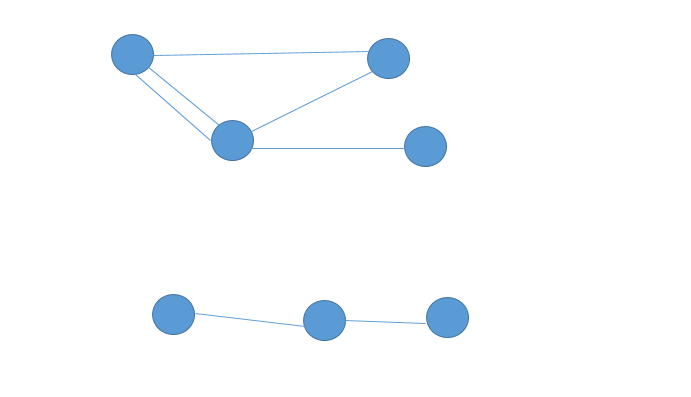
关注
码龄 粉丝数 原力等级 --
- 被采纳
- 被点赞
- 采纳率
已结题
Spark GraphX 中 PageRank 图算法对于图中有些顶点与其他顶点不连通的情况适用么?
收起
- 写回答
- 好问题 0 提建议
- 关注问题
 微信扫一扫点击复制链接
微信扫一扫点击复制链接分享
- 邀请回答
- 编辑 收藏 删除
- 收藏 举报
3条回答 默认 最新
- 关注
码龄 粉丝数 原力等级 --
- 被采纳
- 被点赞
- 采纳率
 devmiao 2018-03-07 16:11关注本回答被题主选为最佳回答 , 对您是否有帮助呢? 本回答被专家选为最佳回答 , 对您是否有帮助呢? 本回答被题主和专家选为最佳回答 , 对您是否有帮助呢?解决 无用评论 打赏举报
devmiao 2018-03-07 16:11关注本回答被题主选为最佳回答 , 对您是否有帮助呢? 本回答被专家选为最佳回答 , 对您是否有帮助呢? 本回答被题主和专家选为最佳回答 , 对您是否有帮助呢?解决 无用评论 打赏举报 微信扫一扫点击复制链接
微信扫一扫点击复制链接分享
评论按下Enter换行,Ctrl+Enter发表内容
报告相同问题?
提交
- 2021-08-07 11:02Vicky_Tang的博客 ConnectedComponents即连通体算法用id标注图中每个连通体,将连通体中序号最小的顶点的id作为连通体的id。 图关系如下时: //创建点 val vertexRDD: RDD[(VertexId, (String,Int))] = SC.makeRDD(Array( (1L...
- 2020-08-05 14:22NICEDAYSS的博客 Spark GraphX 图算法: 一:PageRank模型: 每个网页为一个点 A到B的链接抽象为一条有向边 整张网页链接抽象成一份有向图 接下来我们通过一个转移矩阵来表示用户从页面i到页面j的可能性 M=...
- 2022-10-20 12:00小二上酒8的博客 Spark GraphX是一个分布式图处理框架,基于Pregel接口实现了常用的图算法。包括 PageRank、SVDPlusPlus、TriangleCount、 ConnectedComponents、LPA 等算法,以下通过具象化的图实例理解相应的算法用途。
- 2020-11-27 08:55蜂蜜柚子加苦茶的博客 基于Spark GraphX的图形数据分析为什么需要图计算图(Graph)的基本概念图的术语(一)图的术语(二)图的术语(三)图的术语(四)图的经典表示法Spark GraphX简介GraphX核心抽象GraphX API示例属性图应用示例(一...
- 2025-12-12 16:14酒城译痴无心剑的博客 本次实战基于 Spark GraphX 构建学术用户关系网络图,通过 HDFS 加载顶点与边数据,使用 Graph()、fromEdges() 和 fromEdgeTuples() 三种方式创建图对象,并完成缓存管理、数据查询、属性转换、结构重构及外部数据...
- 2020-11-26 19:46Zhuuu_ZZ的博客 Pregel一 PageRank算法实例实现PageRank算法原理剖析二 ConnectedComponents数据准备图结构实现扩展参考三 Pregelpregel函数源码顶点的激活态和钝化态pregel原理分析pregel代码实现代码分析参考: 一 PageRank算法 ...
- 2025-09-29 23:57Golang编程笔记的博客 本文聚焦Spark生态中的GraphX,全面解析其设计原理、核心功能、算法实现及实战应用,帮助读者掌握分布式图计算的核心思想,理解GraphX与Spark生态的深度整合,掌握基于GraphX的复杂图分析方法。基础概念。
- 2021-03-12 11:37修行修心的博客 Spark GraphX 自带的图算法
- 2021-06-09 23:54weixin_47134119的博客 Spark GraphX概述第2节 Spark Grap2.1 GraphX 架构2.2 存储模式2.3 核心数据结构1、Graph2、vertices3、edges4、triplets第3节 Spark GraphX计算案例一:图的基本操作案例二:连通图算法案例三:寻找相同的用户,...
- 2021-01-17 16:45May--J--Oldhu的博客 完整的PageRank算法(1)完整的PageRank算法思想(2)完整算法数据说明(3)算法公式三.Spark Graphx调用pagerank API四.其他补充1.PR值的决定因素2.获得高pagerank值的方法 一.PageRank基本概念 1.什么是pagerank?...
- 2024-08-28 09:38武子康的博客 GraphX 提供了多种分区方式:边分区(默认,简单但可能产生倾斜)、顶点分区(适合顶点度不均匀的图)、以及 2D 分区(能有效减少通信量)。在实际应用中,可以通过 graph.partitionBy() 显式指定策略,并结合运行时...
- 2024-08-28 08:31武子康的博客 GraphX 与 RDD 深度集成,可直接利用 Spark 的分布式计算能力,同时通过数据切片、消息压缩和图分区等技术进行性能优化,在处理大规模图数据时具备高效性。其架构设计兼顾了图计算的灵活性与可扩展性,使其既能满足
- 2024-03-28 07:36不二人生的博客 利用GraphX自带的社会网络数据集实例,用户集合数据集存在/usr/local/Spark/data/graphx/users.txt,用户关系数据集存在/usr/local/Spark/data/graphx/followers.txt。静态的PageRank算法运行在固定的迭代次数,动态...
- 2024-09-02 02:23教雅思的移民律师的博客 目前已经更新到了:Hadoop(已更完)HDFS(已更完)MapReduce(已更完)Hive(已更完)Flume(已更完)Sqoop(已更完)Zookeeper(已更完)HBase(已更完)Redis (已更完)Kafka(已更完)Spark(正在更新!...
- 2022-04-30 09:49办公模板库 素材蛙的博客 在本模块中,我们将学习 Spark 如何处理图,也就是 Spark 的图挖掘套件 GraphX。虽然图这种数据结构在最近几年中,越来越多地出现在业务场景中,但平心而论,图的使用频率相比前面所学的内容还没有那么频繁。但是,...
- 2019-12-24 11:28综上所述,通过对Spark GraphX的深入源码分析,可以看出GraphX是如何结合Pregel和GraphLab的优点,将图计算与Spark的大数据处理能力相结合的。同时,GraphX通过提供各种图运算操作、优化存储结构和利用Pregel API等...
- 2019-04-30 19:36
大数据技术之_19_Spark学习_05_Spark GraphX 应用解析 + Spark GraphX 概述、解析 + 计算模式 + Pregel API + 图算法参考代码 + PageRank
黑泽君的博客 大数据技术之_19_Spark学习_05_Spark GraphX 应用解析 + Spark GraphX 概述、解析 + 计算模式 + Pregel API + 图算法参考代码 + PageRank - 没有解决我的问题, 去提问