风神大腿 2018-03-20 02:57 采纳率: 50%
浏览 2993
已采纳

范德波尔方程matlab编程

图片说明
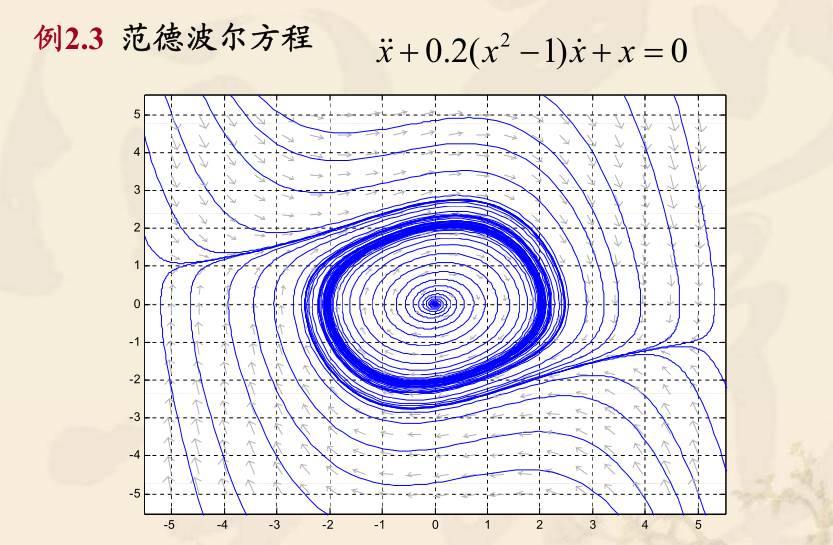
如图求范德波尔方程的matlab仿真图

  • 写回答

1条回答 默认 最新

  • threenewbee 2018-03-21 16:05
    关注

    http://www.pudn.com/Download/item/id/1982307.html
    采纳可以代下。

    本回答被题主选为最佳回答 , 对您是否有帮助呢?
    评论

报告相同问题？

  • m_files.zip_keepuwe_unlesspqo_范德波尔_范德波尔 matlab_范德波尔方程求解
    2022-07-15 01:30
    范德波尔方程求解，采用龙格库塔方法，使用matlab中ode命令编程计算
  • 范德波尔振荡器Simulink模型-Van der Pol Oscillator Simulink Model-matlab
    2025-03-20 18:11
    该Simulink模型表示由以下微分方程描述的范德波尔振荡器 x'-m（1-x^2）x'+x=0 其中x=x（t）是时间的函数，m是物理参数。 人们可以很容易地观察到，对于m=0，系统变为线性。 建议用户尝试m的不同值，并查看系统行为中...
  • 范德波尔振荡器 Matlab 或者 Python 仿真。
    2022-05-09 18:11
    fK0pS的博客 范德波尔振荡器 Matlab 或者 Python 仿真。 参考： https://zh.m.wikipedia.org/zh-hans/%E8%8C%83%E5%BE%B7%E6%B3%A2%E5%B0%94%E6%8C%AF%E8%8D%A1%E5%99%A8 ----------------------------------------------...
  • 范德波尔方程相轨迹与阻尼系统分析
    2025-09-14 07:04
    u8v9w0x1y的博客 本文介绍了使用ode23对范德波尔方程进行数值求解的方法，并分析了不同阻尼系数对弹簧-质量-阻尼器系统响应的影响。包括欠阻尼、临界阻尼和过阻尼状态的特性。同时涉及杜芬振子模型的仿真分析及部分导数计算。
  • 如何理解范德波尔方程
    2022-05-09 16:38
    fK0pS的博客 如何理解范德波尔方程 是荷兰物理学家巴尔塔萨·范·德·波尔在1927年发现的真空管放大器的极限环振荡现象[1]。极限环振荡可以用下列非线性微分方程表示： 电流随时间的变化，服从一下的规律。 我...
  • 范德波尔方程可视化
    2023-07-07 17:07
    sjtuSecondSilly的博客 Van der Pol方程是一个非线性方程， 对于非线性方程， 我们目前还没有通用的工具分析， 但如果把比例尺放大， 只在平衡点附近观察， 更细致地观看平衡点(0,0)附近， 同时缩小仿真仿真的时间，我们会发现平衡点附近该...
  • matlab中使用ode方法解范德波尔微分方程的数值解
    2020-02-06 14:48
    梧桐雪的博客 微分方程的解析解要求比较严苛，只有在特定的条件下才能写出解析解表达式，而在现实的科研问题当中，绝大多数...我们将通过范德波尔方程为例演示求解的过程。大致可以分为2步：列方程和解方程。 一、列方程。 范德波...
  • 在matlab中使用dsolve函数解范德波尔二阶微分方程
    2020-02-05 22:41
    梧桐雪的博客 荷兰物理学家范德波尔为了描述三极管的震荡效应创建了范德波尔方程，其数学表达式如下： 我们假设μ=0,并给给出初始变量的值，可以简化方程如下： 我们把以上数学公式转换成matlab语言并且做出图像如下： syms y(t...
  • 不使用常微分方程模拟范德波尔振荡器_matlab_模拟_Simulation
    2022-05-30 17:11
    在本案例中，我们将探讨如何在MATLAB环境中不使用常微分方程（ODEs）来模拟范德波尔振荡器。 传统的范德波尔振荡器模型通常由以下两个耦合的常微分方程组成： \[ \frac{dx}{dt} = y \] \[ \frac{dy}{dt} = \mu (1 ...
  • MATLAB 数学应用 微分方程
    2021-06-29 11:42
    结冰架构的博客 本文演示了如何使用 MATLAB 构造几种不同类型的微分方程并求解。MATLAB 提供了多种数值算法来求解各种微分方程： 初始值问题 边界值问题 时滞微分方程 偏微分方程 初始值问题 vanderpoldemo 是用于定义 van der ...
  • fni matlab,使用Matlab求解Van Der Pol方程的方法研究
    2021-03-18 05:20
    随缘随喜的博客 维普讯资http/:/wwwcq.vip.ocm02年2月 0 7脑电学习第1期使用 Ma at求解bV n D ...出了三种求微解分方程值数解方的法 .给分别是：用真仿方框图求解： bt教函解求；用S函教求解 对.使用三种方 法解求微方分程进了行较...
  • 使用matlab的仿真器，仿真范德波振子
    2022-05-11 10:38
    fK0pS的博客 使用matlab的仿真器，仿真范德波振子 https://ww2.mathworks.cn/matlabcentral/mlc-downloads/downloads/submissions/46595/versions/3/screenshot.jpg Van der Pol Oscillator Simulink Model - File ...
  • matlab仿真动力学方程的几种方法，总结，以范德波振子为例
    2022-05-12 11:44
    fK0pS的博客 1、 直接写方程 diff(y, 2) == k*(1 - y^2)*diff(y) - y，借助 odeToVectorField 和matlabFunction 和ode45函数求解。优点是，构造的方程非常直接； syms y(t); [V] = odeToVectorField(diff(y, 2) == k*(1 - y^2)*...
  • Van der Pol Oscillator Simulink Model：Simulink 中的 Van der Pol Oscillator 非线性模型。-matlab开发
    2021-05-30 01:15
    参考： [1] 使用 Matlab 的控制理论应用介绍， https://www.researchgate.net/publication/281374146_An_Introduction_to_Control_Theory_Applications_with_Matlab [2] 微分方程、动力学系统和混沌简介，Hirs
  • 范德波尔波形
    2021-01-25 18:02
    「已注销」的博客 function fy=VDP(t,x) fy=[x(2);7*(1-x(1)^2)*x(2)-x(1)]; Y0=[1;0]; [t,x]=ode45(‘VDP’,[0,40],Y0); y=x(:,1); dy=x(:,2);... MATLAB概率与数据统计分析—张德丰等编著–第12页–[M]北京：机械工业出版社
  • 微分方程matlab程序
    2011-03-06 00:50
    ### 微分方程Matlab程序详解 #### 一、微分方程数值解与轨线图绘制 根据提供的信息，这段代码主要涉及了几个不同的微分方程系统的数值求解及其轨线图的绘制。这里我们将逐一分析并解释每个部分。 ### 二、微分...
  • 使用 MATLAB之parfor 在参数扫描过程中绘图.pdf
    2025-01-07 09:02
    本篇文章介绍了如何利用MATLAB的parfor循环以及DataQueue在并行计算中监控进度并实时绘图，特别以范德波尔振荡器为案例详细说明了整个过程。 首先，范德波尔振荡器是一个经典的物理模型，它可以用一组常微分方程来...
  • matlab 中vdp,VDP方程在Simulink仿真中的解析.pdf
    2021-04-26 15:35
    爱生活的马克君的博客 nbspUML理论/建模VDP方程在Simulink仿真中的解析.pdf4页本文档一共被下载：次,您可全文免费在线阅读后下载本文档。 下载提示1.本站不保证该用户上传的文档完整性，不预览、不比对内容而直接下载产生的反悔问题本站...
  • 没有解决我的问题, 去提问