RSA等非对称加密解密的问题

Question

已知明文为123
用私钥加密123得到密文456
（不使用数据填充，每次加密相同的明文都会得到相同的密文）
使用公钥解密456会得到123
我的问题是
已知公钥和明文123能计算出私钥加密生产的密文456吗

Answer 1

1、非对称公钥体制的两个用途：

（1）做加密使用，保障数据的机密性。采用公钥加密，私钥加密。只有私钥才能解密，所以保障了数据的机密性。

（2）做签名使用，进行身份认证。采用私钥加密，公钥解密。公钥公开，任何人都可以对数据进行签名验证，这时的私钥加密的数据只是作为一个
只有拥有私钥的人才能生成的认证符号，所以能够进行对拥有私钥的人进行身份认证。签名原理如图：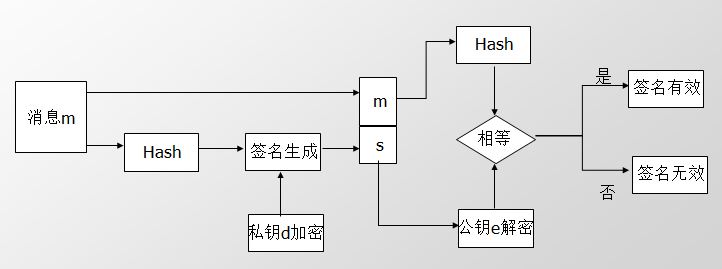

你的这个问题一个是第二种情况，用作数字签名使用的。已知公钥和明文是不能计算出密文的，一般商用的密钥长度都要求达到1000比特才能保证
RSA密码的安全性，你举的例子太过简单，如果私钥过短，是可以使用穷举搜索攻击得出私钥，从而得到加密的密文的。假设我们在密钥长度达到安全性要求的前提下进行讨论，已知公钥和明文是不能计算出密文的。

2.RSA算法的理论基础
大数分解：两个大素数相乘在计算上是容易实现的，但将该乘积分解为两个大素数因子的计算量却相当巨大。
素数检测：素数检测就是判定一个给定的正整数是否为素数。

3.签名的过程：设计密钥，设计签名，验证签名
(1)设计密钥
1)随机产生两个不同的大素数p和q，计算n=p x q和ψ(n)=(p-1)(q-1);
2)随机选择数e，满足1<e<ψ(n),且gcd(e,ψ(n))=1（e和ψ(n)的最大公约数为1）,那么公钥就是(e,n);
3)计算d，满足ed=1modψ(n)，私钥就是d；
(2)设计签名
签名s=明文的d次方 mod n
(3)验证签名
取得发送方的公钥(e，n)，明文=签名s的e次方 mod n;在将计算出来的明文和接收方收到的明文做对比，两者一致，说明签名有效。

4 RSA算法的安全性依赖于大数分解困难性。
原理：
假设在知道公钥(e,n)的条件下，我们能进行大数分解，即找到两个不同的大素数p和q，使得n=p x q，那么ψ(n)=(p-1)(q-1)可以计算出来，
那么由ed=1modψ(n)，可以计算出私钥d；私钥d计算出来后，通过：密文s=明文的d次方 mod n可以计算出密文。

5 结论：在密钥长度达到安全性的条件下，大数分解具有困难性，因此RSA公钥体制是安全的。