Problem Description
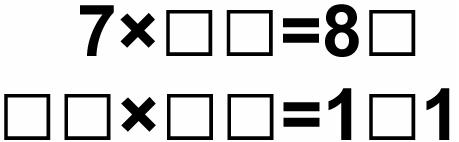
If you hide some digits in an integer equation, you create a digit puzzle. The figure below shows two valid digit puzzles.Hidden digits are represented by squares, and other digits are shown. The numbers involved in this problem are all positive integers, written in decimal forms without leading zeros.
If a digit puzzle has a unique solution, we call it a good puzzle. Both puzzles shown above are good puzzles. The solution to the first puzzle is 7*12=84, while the solution to the second one is 11*11=121. You are already given some digit puzzles, but some of them are not good. Your task is to convert these puzzles into good ones. You can change any wildcard character (i.e. hidden digits) into a real digit, any real digit to a wildcard character, or
a real digit to another real digit, but you cannot insert or remove any character at any place. The number of changed characters should be minimized. In this problem, the puzzle is always in the form "a x b = c", and "a x b" and "b x a" should be considered different if a is not equal to b. It is allowed that all digits of both a and b are shown (e.g 12 x 34 = ****), though that puzzle is actually a simple multiplication problem. Write a program to make good puzzles.
Input
The input contains several test cases. Each test case contains three non-empty strings, x, y, z, having at most 2, 2 and 4 characters respectively. Each character is a digit or a wildcard '*', x will not begin with a zero character. The last test case is followed by a single zero, which should not be processed.
Output
For each test case, print the case number and the converted puzzle. If more than one optimal solution is found, the lexicographically first one should be printed (remember that "*" is before "0"). There is always a solution.
Sample Input
7 ** 8*
0
Sample Output
Case 1: 7 ** 8*
Case 2: ** ** 1*1