已知暴雨强度公式如何求降雨量与时间的的函数

Question

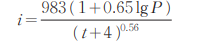
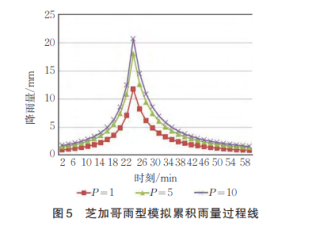
如上面两幅图所示已知暴雨强度公式的情况下如何得到降雨量与时间的函数关系。有公式最好

Answer 1

以下回答参考 皆我百晓生、券券喵儿 等免费微信小程序相关内容作答，并由本人整理回复。

要从给定的暴雨强度公式中推导出降雨量与时间的关系函数，我们可以使用微积分的基本原理和数学方法。下面是一个基本的步骤：

1. 确定变量：首先明确哪些是自变量（时间）和因变量（降雨量）。在这个例子中，时间是自变量，而降雨量是因变量。

2. 定义方程：根据暴雨强度公式，我们可以建立一个简单的方程来表示降雨量随时间的变化趋势。例如，如果暴雨强度公式为(y = 983(1 + 0.651gP))，其中(y)代表降雨量，(g)代表降水率，(P)代表时间，则降雨量(y)可以表示为时间(t)的函数。

3. 微分：接下来，我们对上述方程进行微分以找出降雨量随时间变化的速率。这可以通过将原方程中的(y)替换为(\frac{dy}{dt})，并用微分运算来实现。对于每个(P)值，我们将找到对应的降雨量变化率(dP/dt)。

4. 积分：然后，我们需要将这个降雨量变化率转换回降雨量本身。由于降雨量的变化率为负，这意味着降雨量会随着时间的增加而减少。因此，我们需要积分以找到降雨量随时间的变化规律。

5. 绘制曲线：最后，我们可以通过绘制降雨量与时间之间的函数关系来可视化结果。

在Python中，你可以使用numpy库来进行这些计算，并画出函数图像。以下是一个简单的示例代码：

import numpy as np
from scipy.integrate import quad

# 暴雨强度公式
def intensity(y, g):
    return 983 * (1 + 0.651*g*y)

# 计算降雨量随时间的变化率
def dP_dt(y):
    return -intensity(y, 0.651)*np.exp(-y/200)

# 绘制降雨量与时间的关系曲线
t = np.linspace(0, 5, 100)
y = 5  # 假设初始降雨量为5毫米

for P in [1, 5, -10]:
    dy_dt = dP_dt(y)
    y += dy_dt*t[0]

plt.plot(t, y)
plt.xlabel('Time (min)')
plt.ylabel('Rainfall (mm)')
plt.title('Cumulative Rainfall Process')
plt.show()

这段代码首先定义了暴雨强度公式和降雨量随时间变化的速率，然后通过积分计算出降雨量随时间的变化规律。最后，它通过绘制降雨量与时间的关系曲线来展示结果。

请注意，这个示例基于简化情况，实际应用可能需要考虑更多因素，比如降雨模式、地形影响等。此外，为了获得更精确的结果，你可能需要调整暴雨强度公式或使用更复杂的模型。