matlab 2019b 求2ask求包洛的高阶达不到论文的要求，不知道那错了

Question

clear all
close all
A1 = [];   %这个矩阵用来装J 循环100次的值
for a1=1:1:100
i=5;                                %5个码元
j=5000;
t=linspace(0,5,j);                  %0-5之间产生5000个点行矢量，即分成5000份
fc=550;                              %载波频率
fm=(i.*200)/4;                             %码元速率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%产生基带信号
x=(rand(1,i))                       %rand函数产生在0-1之间随机数，共1-10个
a=round(x);                         %随机序列，round取最接近小数的整数
st=t;
for n=1:i
    if a(n)<1
        for m=j/i*(n-1)+1:j/i*n
            st(m)=0;
        end
    else
        for m=j/i*(n-1)+1:j/i*n
            st(m)=1;
        end
    end
end
figure(1);
subplot(421);
plot(t,st);                         %基带信号函数
axis([0,5,-0.2,1.2]);
title('基带信号st');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
s1=cos(2*pi*fc*t);                  %载波
subplot(422);
plot(t,s1);                         %载波信号函数
axis([0,5,-1,1]);
title('载波信号s1');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
e_2ask=st.*s1;                      %调制
subplot(423);
plot(t,e_2ask);                     %调制信号函数
axis([0,5,-1,1]);
title('已调信号e_2ask');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
SNR=15;                                    %定义信噪比，单位DB 
sigpow=mean(abs(e_2ask).^2);                       %power of input signal
noisefac=10^(-SNR/10);
noise=randn(1,size(e_2ask,2));
noise=noise*(sqrt(sigpow*noisefac)/sqrt(mean(noise.^2)));      %产生所需的高斯噪声
ynoise=noise+e_2ask;                               %加噪后的信号
subplot(424);
plot(t,ynoise);                          %噪声信号函数
axis([0,5,-1,2]);
title('加入噪声后的信号'); 

yh = hilbert(ynoise);    % matlab函数得到信号是合成的复信号
A = abs(yh);                          %带噪声信号的包络
c=bandpower(e_2ask) ;                 %求已调信号的功率
C=mean(A);                              %包洛的期望

D=mean(A.^4);               %包洛4次方的期望
E0=mean(A.^2);              %包洛2次方的期望
E=2*(E0.^2);
fz=(D-E);
fm=(4.*c.*c);
J=fz/fm;
A1 = [A1,J]; 
end
max=(max(A1));
min=(min(A1));
A2=mean(A1,2);
E3=mean(A1);

按理论条件信噪比大于15db时，信号的高阶包洛特征，应该趋近于0，且波动很小，但我算出来100个的J值，在-0.7到3之间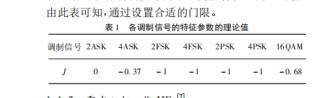

且我个人认为，包洛应该不收信号的频率这些的影响，只和A（幅度）有关

下面是我参考论文公式

假设接收到的信号为

f( t) = s( t) + n( t) = A( t) cos［( t) ］+ n( t)   （1）