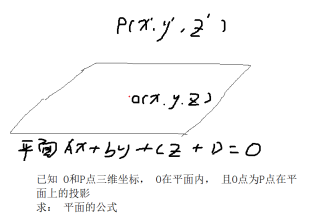
已知o,p两点的三维坐标，且O为P点在某平面的投影，求平面公式

Question

已知o,p两点的三维坐标，

且O为P点在某平面的投影，

求平面公式

方法或者python 代码等

 

Answer 1

思路如下：

求出两个垂直于向量op的不共线的向量v1和v2，根据这两个向量得到点p1和p2，加上o点，通过三点得到平面方程的4个参数。

# -*- coding: utf-8 -*-

import numpy as np

def get_ortho(op):
    """返回垂直于向量op的两个向量"""
    
    if not op.any(): # 向量op的每一个元素都是0
        return None
    
    i = np.where(op!=0)[0][0] # 向量op的第1个不为0的元素的索引号
    v1 = np.ones(op.shape, dtype=np.float64) # 构造一个元素全部为1的向量
    v2 = np.arange(op.size, dtype=np.float64) # 构造一个元素递增的向量
    v1[i] = 0 # 令第i个元素为0
    v2[i] = 0 # 令第i个元素为0
    v1[i] = -np.dot(op,v1)/op[i]
    v2[i] = -np.dot(op,v2)/op[i]
    
    return v1, v2

def get_plane_by_three_point(p1, p2, p3):
    """根据三点坐标返回平面方程"""
    
    x1, y1, z1 = p1
    x2, y2, z2 = p2
    x3, y3, z3 = p3
    
    a = (y2-y1)*(z3-z1) - (y3-y1)*(z2-z1)
    b = (z2-z1)*(x3-x1) - (z3-z1)*(x2-x1)
    c = (x2-x1)*(y3-y1) - (x3-x1)*(y2-y1)
    d = a*x1 - b*y1 - c*z1
    
    return a, b, c, d

def demo(o, p):
    """点o为点p在某平面的投影，计算该平面方程"""
    
    o = np.array(o)
    p = np.array(p)
    
    op = p - o
    v1, v2 = get_ortho(op)
    p1 = o + v1
    p2 = o + v2
    a, b, c, d = get_plane_by_three_point(p1, p2, o)
    
    print('%fx + %fy + %fz + %f = 0'%(a, b, c, d))

if __name__ == '__main__':
    o, p = (0,0,0), (1,0,0)
    demo(o, p)
    o, p = (1,2,3), (3,5,2)
    demo(o, p)