若已知p为2017k+1型素数，如何证明一定存在x使原方程成立

Question

 

Answer 1

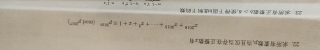
为了证明当
𝑝
p为
2017
𝑘
+
1
2017k+1型素数时，一定存在
𝑥
x使得某个方程成立，我们需要首先明确方程的具体形式。不过，由于您没有提供具体的方程，我将给出一个通用的证明框架，您可以根据具体的方程进行调整。

假设我们的方程是
𝑓
(
𝑥
)
≡
0
(
m
o
d
𝑝
)
f(x)≡0(modp)，其中
𝑓
(
𝑥
)
f(x)是一个关于
𝑥
x的多项式。

第一步，根据题目信息，我们知道
𝑝
p是
2017
𝑘
+
1
2017k+1型的素数。

第二步，根据费马小定理，如果
𝑝
p是素数且
𝑎
a不是
𝑝
p的倍数，则
𝑎
𝑝
−
1
≡
1
(
m
o
d
𝑝
)
a
p−1
≡1(modp)。

第三步，由于
𝑝
p是
2017
𝑘
+
1
2017k+1型的，我们有
𝑝
−
1
=
2017
𝑘
p−1=2017k。

第四步，考虑
𝑓
(
𝑥
)
f(x)的某个特定的非零根
𝑎
a（如果存在的话）。根据费马小定理，我们有
𝑎
2017
𝑘
≡
1
(
m
o
d
𝑝
)
a
2017k
≡1(modp)。

第五步，由于
𝑎
2017
𝑘
≡
1
(
m
o
d
𝑝
)
a
2017k
≡1(modp)，我们可以得出
𝑓
(
𝑎
)
≡
0
(
m
o
d
𝑝
)
f(a)≡0(modp)。

第六步，如果
𝑓
(
𝑥
)
f(x)没有非零根，那么我们需要考虑其他方法，比如使用多项式在模
𝑝
p意义下的性质，如拉格朗日插值法或其他代数技巧。

第七步，如果
𝑓
(
𝑥
)
f(x)是一个线性方程，那么我们可以直接使用模逆元的概念来求解。

第八步，如果
𝑓
(
𝑥
)
f(x)是一个高次方程，我们可能需要使用更复杂的代数技巧，如模意义下的因式分解或利用模
𝑝
p的有限域性质。

第九步，如果
𝑓
(
𝑥
)
f(x)是一个具体的方程，请提供方程的具体形式，以便我们可以给出更具体的证明或解法。

综上所述，为了证明一定存在
𝑥
x使得方程成立，我们需要根据方程的具体形式和性质，结合模数
𝑝
p的性质，进行详细的推导和证明。