LMI约束中有两个sdpvar变量形式的矩阵相乘，发现yalmip工具箱求不出解

Question

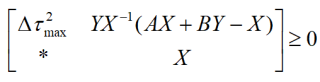
如上图所示的LMI约束，tau是已知的常数，表示沿对角线对应矩阵块的转置，A、B是已知的矩阵，X和Y都是sdpvar变量，想求满足条件的X矩阵和Y矩阵。在用yalmip和sdpt3求解器计算时求不出解，显示NAN。但如果将第一行第二列元素中的Yinv(X)去掉后，能够正常求解。以前也遇到过这样的问题，只要在LMI中遇见两个sdpvar变量相乘时，yalmip都算不出解，请教这是什么原因？

Answer 1

所有内容均由人工智能模型输出，其内容的准确性和完整性无法保证，不代表我的态度或观点。

---

该回答引用文心大模型4.0，仅提供参考，不保证完全正确
目前为文心大模型4.0专栏，网页版本：V2.5.3（2024.1.19）
YALMIP工具箱在处理SDP（半定规划）问题时，通常对决策变量的类型和约束条件有一定的限制。特别是当涉及到两个sdpvar变量相乘时，这可能会导致问题变得非凸，从而难以求解。在许多优化问题中，非凸性是一个主要的挑战，因为它可能导致存在多个局部最优解，或者根本不存在解。

---

在你提供的问题中，Yinv(X)这个表达式可能是一个主要的难点。这个表达式表示Y的逆与X的乘积，而Y和X都是sdpvar变量。这意味着你正在尝试求解一个非线性（且可能是非凸的）半定规划问题。这类问题通常是非常难以求解的，特别是当使用基于内点法的求解器（如SDPT3）时。

---

为了解决这个问题，你可以尝试以下几种方法：

1. 重新表述问题：尝试以不同的方式表述问题，以避免两个sdpvar变量的乘积。例如，你可以尝试引入新的变量和约束来替代这个乘积。
2. 使用不同的求解器：有些求解器可能更适合处理这类非凸问题。你可以尝试使用其他支持非凸优化的求解器，如PENBMI或BMIBNB。
3. 提供初始解：如果可能的话，提供一个合理的初始解可能有助于求解器更快地找到解决方案。
4. 检查问题的可行性：确保你的问题是可行的，即存在至少一个满足所有约束条件的解。你可以通过求解一个简化的问题（例如只包含一部分约束条件）来检查这一点。
5. 分解问题：如果可能的话，尝试将问题分解为更小的子问题，然后分别求解这些子问题。这可能会使问题更容易处理。
6. 咨询专家：如果上述方法都不起作用，你可能需要咨询优化或控制领域的专家以获取更专业的建议。

---

图片转文字可能造成误差，不代表模型真实水平