有人会吗，用matlab实现，画出图像，把所有结果画在一个图上。

Question

用matlab绘制图像代码，这是我写的部分代码

```c#

function v = Interp2021(x,y,u)
n=length(x);
v=zeros(size(u));
    for k=1:n
    w=ones(size(u));
        for j=[1:k-1 k+1:n]
        w=(u-x(j))./(x(k)-x(j)).*w;
        end
        v=v+w*y(k);
    end
 plot(x,y,'o',u,v,'-');   
end

```

Answer 1

你好同学，只需要调用你的函数就行啊：
你的函数：

function v = Interp2021(x,y,u)
n = length(x);
v = zeros(size(u));
for k=1:n
    w=ones(size(u));
    for j=[1:k-1 k+1:n]
        w=(u-x(j))./(x(k)-x(j)).*w;
    end
    v=v+w*y(k);
end
end

我给出的主函数：

clc;clear
x = [4,9,16,25,36,49,64,81,100];
y = [2,3,4,5,6,7,8,9,10];
% 第（1）题
u = 1:1:100; 
for i = 2:9
    subplot(2,4,i-1)
    plot(x,y,'ro'); hold on
    v = Interp2021(x(1:i),y(1:i),u);
    plot(u,v,'b-');
    title([num2str(i-1),'阶Lagrange'])
end
% 第（2）题
clear u;
u = 10:10:200;
vn = arrayfun(@(i)['n=',num2str(i-1)],2:9,'uniform',0);
rn = arrayfun(@(i)['x=',num2str(u(i))],1:numel(u),'uniform',0);
T = table('Size',[numel(u),8],'VariableTypes',repmat("double",1,8),'variablenames',vn,'rownames',rn);
format short
for i = 2:9
    v = Interp2021(x(1:i),y(1:i),u);
    T{:,i-1} = v(:);
end
T

最后画图结果：

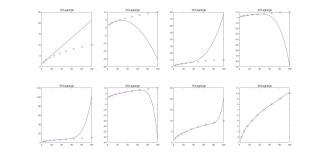
最后输出各阶插值在x=10，20，30，……，200 的插值

T =

  20×8 table

             n=1       n=2       n=3        n=4       n=5        n=6       n=7        n=8  
             ____    _______    ______    _______    ______    _______    ______    _______

    x=10      3.2     3.1714    3.1667      3.165    3.1643     3.1639    3.1636     3.1634
    x=20      5.2     4.3619     4.455     4.4656    4.4686     4.4699    4.4705     4.4709
    x=30      7.2        4.6    5.6111     5.4962    5.4838     5.4805    5.4792     5.4785
    x=40      9.2     3.8857    7.4286     6.2208    6.3075     6.3186    6.3217     6.3229
    x=50     11.2      2.219    10.701     5.8817    7.0927     7.0754    7.0726     7.0718
    x=60     13.2       -0.4    16.222          3    8.6957     7.8007    7.7593     7.7511
    x=70     15.2    -3.9714    24.786     -4.625    13.323     7.9387    8.3119      8.351
    x=80     17.2    -8.4952    37.185    -19.915    25.179     5.2089    8.9009      8.936
    x=90     19.2    -13.971    54.214    -46.515    51.115    -6.0681    11.111     9.6416
    x=100    21.2      -20.4    76.667    -88.788    101.27      -37.2      20.4         10
    x=110    23.2    -27.781    105.34    -151.82    189.74    -107.91    50.294     6.6963
    x=120    25.2    -36.114    141.02    -241.42    335.18    -249.66    128.76    -11.486
    x=130    27.2      -45.4     184.5    -364.12     561.5    -509.58    307.23    -73.111
    x=140    29.2    -55.638    236.58    -527.18     898.5    -954.88    672.67    -239.85
    x=150    31.2    -66.829    298.06    -738.55    1382.5    -1677.9    1363.2    -630.83
    x=160    33.2    -78.971    369.71    -1006.9      2057    -2801.5    2587.8    -1458.1
    x=170    35.2    -92.067    452.35    -1341.8    2973.3    -4485.6      4650    -3076.5
    x=180    37.2    -106.11    546.76    -1753.1    4191.2    -6933.2    7977.3    -6050.4
    x=190    39.2    -121.11    653.74      -2252    5779.7     -10398     13155     -11242
    x=200    41.2    -137.07    774.07    -2849.8    7817.4     -15193     20966     -19925

可见高阶拉格朗日插值虽然前面精度很高，但是到了后面基本上都是误差极大。
有帮助还望题主给个采纳支持一下答主呢，谢谢啦