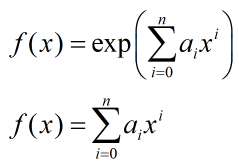用指数多项式去拟合一组数据，用最小二乘法求解参数，如何加上0到40的积分为1这个约束

Question

下图分别为指数多项式和普通多项式的公式，去拟合一组数据（x,y），约束条件为积分是1。如果是普通多项式去拟合这组数据的话，可以把约束中的积分变成等式，用拉格朗日乘子法+最小二乘法去求参数（如下面这个代码）。但如果是指数多项式拟合这组数据的话，不考虑约束，只要把y取个对数就能用最小二乘法算出参数，但考虑约束的话，这个指数积分是求不出来的，无法化为等式，那积分为1这个约束条件，要如何去满足

x = [0:5:40]; % x随意
y = pi/80*sin(1/40*pi*x)+(rand(size(x))-0.5)*pi/80*1/2;% y随意设置，在正弦函数上加随机浮动
n = 5; % n随意
x = x(:);
y = y(:);
S = zeros(length(x), n+1);
q = ones(length(x),1);
S(:,n+1)=q;
for i = n:-1:1
    q = q.*x;
    S(:,i) = q;
end
A = S'*S;
b = S'*y;
a = A\b;%最小二乘
G = 1./(n+1:-1:1).*40.^(n+1:-1:1); % 
aa = [A, G'; G, 0]\[b;1];%拉格朗日乘子法

Answer 1

你好同学，建议从积分得到的非线性方程考虑，或者先由最小二乘得到正数表达式，然后用积分考虑改变前面的系数除以一个比例就行（实质是改变a0）。
方法1 非线性方程组方法：

x = [0:1:40]; % x随意
mu = 20; sigma = 10;
y = 1/sqrt(2*pi)/sigma*exp(-(x-mu+rand(size(x))*2).^2/2/sigma^2);% y随意设置，在正弦函数上加随机浮动
y(y<=0) = 10*eps;
n = 5; % n随意
x = x(:);
y = y(:);
S = zeros(length(x), n+1);
q = ones(length(x),1);
S(:,n+1)=q;
for i = n:-1:1
    q = q.*x;
    S(:,i) = q;
end
logy = log(y);
A = S'*S;
b = S'*logy;
a = A\b;%最小二乘
ff = @(x,a) exp(polyval(a,x));
eq = @(a)[A*a-b; integral(@(x)ff(x,a),0,40)-1];%构建了方程组后面一项指的是积分为1
options = optimoptions('fsolve','Display','off','FunctionTolerance',1e-2,'algorithm','levenberg-marquardt');
[a, f, flag] = fsolve(eq, a, options);
while (flag>=4 || flag<=0)
    [aa, f, flag] = fsolve(eq, a+a.*(2*rand(size(a))-1), options);
end
a = aa;
xfit = linspace(min(x),max(x),1001);
plot(x,y,'r-',xfit,exp(polyval(a,xfit)),'b-')
legend('原值','拟合后')

效果

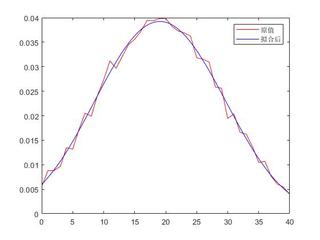
但是这种方法计算慢，有的时候很难找到满意的解。

方法2 比例系数法：
先用最小二乘法，然后得到的结果积分出来得到积分值S，然后整体拟合函数除以S（或者a0=a0-log(S)）

x = [0:1:40]; % x随意
mu = 20; sigma = 10;
y = 1/sqrt(2*pi)/sigma*exp(-(x-mu+rand(size(x))*2).^2/2/sigma^2);% y随意设置，在正弦函数上加随机浮动
y(y<=0) = 10*eps;
n = 5; % n随意
x = x(:);
y = y(:);
S = zeros(length(x), n+1);
q = ones(length(x),1);
S(:,n+1)=q;
for i = n:-1:1
    q = q.*x;
    S(:,i) = q;
end
logy = log(y);
A = S'*S;
b = S'*logy;
a = A\b;%最小二乘
ff = @(x,a) exp(polyval(a,x));
S = integral(@(x)ff(x,a),0,40);
a(end) = a(end) - log(S);%整体除以S
xfit = linspace(min(x),max(x),1001);
plot(x,y,'r-',xfit,exp(polyval(a,xfit)),'b-')
legend('原值','拟合后')

效果：

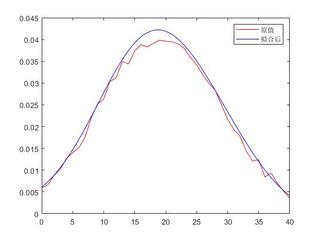
这种方法快捷简便，而且形状很容易抓住，但是有的点拟合对不上，可能拟合效果不会很好，但是整体趋势是不会错的，算法也稳健。