下图为多元指数多项式,去拟合一组数据(x,y,f(x,y)),约束条件为x在0到40,y在0到360(xy的范围最好可变),f(x,y)的积分等于1。
一维的指数多项式,拟合一组数据,积分为1的方法,可以用非线性方程组方法和比例系数法,为下面2个程序。然后二维数据的多元指数多项式不带积分为1的程序也在下面写了,如果把一维指数多项式的非线性方程组方法和比例系数法用在二维数据里,要如何编写,写了一半的程序和仿造的程序都在下面。
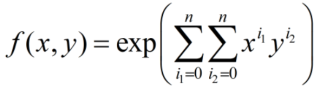
一维指数多项式积分为1,非线性方程组法
x = [0:1:40]; % x随意
mu = 20; sigma = 10;
y = 1/sqrt(2*pi)/sigma*exp(-(x-mu+rand(size(x))*2).^2/2/sigma^2);% y随意设置,在正弦函数上加随机浮动
y(y<=0) = 10*eps;
n = 5; % n随意
x = x(:);
y = y(:);
S = zeros(length(x), n+1);
q = ones(length(x),1);
S(:,n+1)=q;
for i = n:-1:1
q = q.*x;
S(:,i) = q;
end
logy = log(y);
A = S'*S;
b = S'*logy;
a = A\b;%最小二乘
ff = @(x,a) exp(polyval(a,x));
eq = @(a)[A*a-b; integral(@(x)ff(x,a),0,40)-1];%构建了方程组后面一项指的是积分为1
options = optimoptions('fsolve','Display','off','FunctionTolerance',1e-2,'algorithm','levenberg-marquardt');
[a, f, flag] = fsolve(eq, a, options);
while (flag>=4 || flag<=0)
[aa, f, flag] = fsolve(eq, a+a.*(2*rand(size(a))-1), options);
end
a = aa;
xfit = linspace(min(x),max(x),1001);
plot(x,y,'r-',xfit,exp(polyval(a,xfit)),'b-')
legend('原值','拟合后')
一维指数多项式积分为1,比例系数法
x = [0:1:40]; % x随意
mu = 20; sigma = 10;
y = 1/sqrt(2*pi)/sigma*exp(-(x-mu+rand(size(x))*2).^2/2/sigma^2);% y随意设置,在正弦函数上加随机浮动
y(y<=0) = 10*eps;
n = 5; % n随意
x = x(:);
y = y(:);
S = zeros(length(x), n+1);
q = ones(length(x),1);
S(:,n+1)=q;
for i = n:-1:1
q = q.*x;
S(:,i) = q;
end
logy = log(y);
A = S'*S;
b = S'*logy;
a = A\b;%最小二乘
ff = @(x,a) exp(polyval(a,x));
S = integral(@(x)ff(x,a),0,40);
a(end) = a(end) - log(S);%整体除以S
xfit = linspace(min(x),max(x),1001);
plot(x,y,'r-',xfit,exp(polyval(a,xfit)),'b-')
legend('原值','拟合后')
多元指数多项式,不带积分为1的约束程序
%% 为了得到分布,假设了一个协方差矩阵
mu=[20,180];%数学期望
sigma=[20/3 0;0,60].^2;%协方差矩阵
r=mvnrnd(mu,sigma,100000);%生成100000个样本
x = r(:,1);
y = r(:,2);
nx = 40;
ny = 40;
xmax = 40;
ymax = 360;
dx = xmax/nx;
dy = ymax/ny;
[X, Y, C, xmid, ymid] = ef2(x,y,nx+1,ny+1,[0,xmax],[0,ymax]);
C = C/(dx*dy);%单位面积上的概率即概率密度
figure(1);clf;
bar3(C)
title('原先数据')
xtick = 1:size(C,2); xticklabel = xmid; % xtick和xticklabel一定要对应,长度相等
ytick = 1:size(C,1); yticklabel = ymid; % ytick和yticklabel一定要对应,长度相等
set(gca, 'xtick', xtick, 'xticklabel',xticklabel,...
'ytick', ytick, 'yticklabel',yticklabel)
xlabel('X')
ylabel('Y')
x = X(:);
y = Y(:);
z = C(:);%根据x和y算出的频率,x,y,z为输入数据
n = 7; % n为多项式的阶数,参数一共为(n+1)²个
[i1, i2] = meshgrid(0:n);
F = arrayfun(@(i)x.^i1(i).*y.^i2(i), 1:numel(i1), 'uniform', 0);
F = cell2mat(F);
F1=[z,F]%这里是因为z数据有时候频率为0,必须把含0的数据去掉
[r,c]=size(F1);
index=1:r; %一维矢量, F1的行指标
all(F1') %将F1转置一下, 返回一个矢量,它的每个元素进行判断, F1所在行的元素全不为0则是1, 否则为0
F1=F1(index(all(F1')),:) %取出F1不含0元素的行,构成新的矩阵
F1(:,1)=[]
z(z==0)=[]
logz=log(z)
A = F1'*F1;
b = F1'*logz;
a = A\b;%最小二乘法
zfit = polyfunval(X,Y,a,n);
zfit1 = exp(zfit);
surf(X,Y,zfit1);%这之后的非线性方程组法和比例系数法如何仿造上面的程序继续
function f = polyfunval(x,y,a,n)%指数多元多项式的公式
[i1, i2] = meshgrid(0:n);
Cfit = arrayfun(@(i)a(i)*x.^i1(i).*y.^i2(i), 1:numel(i1), 'uniform', 0);
f = Cfit{1};
for i = 2:numel(Cfit)
f = f + Cfit{i};
end
end
function [X, Y, CDF, xmid, ymid] = ef2(x,y,nx,ny,xminmax,yminmax)%输入数据,只知道x和y,算出频率z
num = length(x);
if(num~=length(y))
error('输入的x和y长度必须相等')
end
if(nargin>6) % 如果变量个数大于6个,太多了
error('太多输入变量')
elseif(nargin<2) % 如果变量个数小于2个,太少了
error('输入变量数目不足!!')
end
if(nargin==6) % 如果变量个数等于6个,赋值给ymin和ymax
ymin = yminmax(1);
ymax = yminmax(2);
end
if(nargin>=5)% 如果变量个数大于等于5个,赋值给xmin和xmax
xmin = xminmax(1);
xmax = xminmax(2);
end
if(nargin<=4)% 如果变量个数小于等于4个,自定义xmin和xmax
xmin = min(x);
xmax = max(x)+eps;
ymin = min(y);
ymax = max(y)+eps;
end
if(nargin<=3)% 如果变量个数小于等于3个,自定义y方向划分段数ny
ny = 30;
end
if(nargin==2)% 如果变量个数等于2个,自定义x方向划分段数nx
nx = 30;
end
xg = linspace(xmin, xmax, nx);%x方向的点
yg = linspace(ymin, ymax, ny);%y方向的点
xmid = (xg(1:end-1)+xg(2:end))/2;
ymid = (yg(1:end-1)+yg(2:end))/2;
[X,Y] = meshgrid(xmid, ymid);%形成网格
[I,J] = meshgrid(2:nx, 2:ny);%下标网格
CDF = arrayfun(@(i,j)sum(x>=xg(i-1)&x<xg(i)&y<yg(j)&y>=yg(j-1))/num,I,J);%形成经验分布
end
