伙伴们帮帮忙，帮我用这个物理问题编写一个编程，不少于50个语句就行，我是真不会～

Question

现在有一个空心半径为R球放水中恰好淹没了一半，现在把球往下轻轻地按下去，按下的深度是d＜<R，求这个球的运动方程。

Answer 1

你好，比如球半径R=1，重力加速度是9.8

function eulerMain %主函数
R = 1;%半径
g = 9.8;%重力加速度
odefun = @(t,y) [y(2);
    (-3/2*y(1)/R+1/2*(y(1)/R)^3)*g];% 构建微分方程
y0 = [0.01; 0]; % 设置初值y(0)=-0.1m
tspan = [0, 20];% 微分方程求解时间跨度
[t,y] = euler(odefun, tspan, y0);%利用欧拉法求odefun
figure(1);clf
subplot(2,1,1)
plot(t,y(:,1),'r-')%画图
hold on
plot(t,y(:,2),'b--')%画图
xlabel('t')
ylabel('y')
legend('位移','速度')
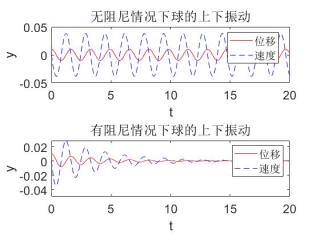
title('无阻尼情况下球的上下振动')
set(gca,'fontsize',16)
c = 0.05; %阻尼设置
odefun = @(t,y) [y(2);
    (-3/2*y(1)/R+1/2*(y(1)/R)^3 -c*y(2))*g ];% 构建微分方程
y0 = [0.01; 0]; % 设置初值y(0)=-0.1m
tspan = [0, 20];% 微分方程求解时间跨度
[t,y] = euler(odefun, tspan, y0);%利用欧拉法求odefun
subplot(2,1,2)
plot(t,y(:,1),'r-')%画图
hold on
plot(t,y(:,2),'b--')%画图
xlabel('t')
ylabel('y')
legend('位移','速度')
title('有阻尼情况下球的上下振动')
set(gca,'fontsize',16)
end
function [t, y] = euler(odefun, tspan, y0)
% odefun ode函数
% tspan: 求解时间范围
% x0：初值
t = tspan(:);
if(numel(tspan)==2)
    t = linspace(tspan(1), tspan(2), 10001)';
end
dy0 = odefun(t(1), y0);
y = zeros(numel(t), numel(dy0));
y(1,:) = y0(:);
for i = 2:1:numel(t)
    y(i,:) = y(i-1,:) + odefun(t(i-1),y(i-1,:))'*(t(i)-t(i-1));%向前欧拉积分
    y(i,:) = y(i-1,:) + (odefun(t(i-1),y(i-1,:))'+ ...
        odefun(t(i),y(i,:))')*(t(i)-t(i-1))/2;%向前欧拉积分
end
end

效果：