背包问题的定义是:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量
内,我们如何选择,才能使得物品的总价格最高。下图是背包问题的一个例子,应该选择哪
些盒子,才能使价格尽可能地大,并且保持总重量不超过 15 kg?所选物品的总价值是多少?
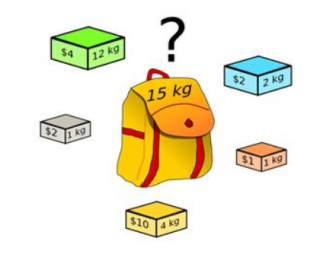
背包问题的定义是:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量
内,我们如何选择,才能使得物品的总价格最高。下图是背包问题的一个例子,应该选择哪
些盒子,才能使价格尽可能地大,并且保持总重量不超过 15 kg?所选物品的总价值是多少?

题主,上一个给你发的那个输入顺序换下就对了,不用重新发题
//一维数组解法
#include<stdio.h>
#define MAX_M 12880 //最大限重
#define MAX_N 3402 // 最大种类数
#define max(a,b) a>b?a:b
int dp[MAX_M + 1]={0};
int weights[MAX_N + 1];
int values[MAX_N + 1];
int main() {
int n, m, i, j;
scanf("%d%d", &n , &m);//n是种类,m是限制重量
for (i = 1; i <= n; i++) {
scanf("%d%d", &values[i],&weights[i] );
}
for (i = 1; i <= n; i++) {
for (j = m; j >= weights[i]; j--) {
dp[j] = max(dp[j], dp[j - weights[i]] + values[i]);
}
}
printf("%d\n", dp[m] );
}
/*
5 15
4 12
2 2
2 1
1 1
10 4
*/