本题要求编写程序,计算N个有理数的平均值。
输入格式:
输入第一行给出正整数N(≤100);第二行中按照a1/b1 a2/b2 …的格式给出N个分数形式的有理数,其中分子和分母全是整形范围内的整数;如果是负数,则负号一定出现在最前面。
输出格式:
在一行中按照a/b的格式输出N个有理数的平均值。注意必须是该有理数的最简分数形式,若分母为1,则只输出分子。
输入样例1:
4
1/2 1/6 3/6 -5/10
输出样例1:
1/6
输入样例2:
2
4/3 2/3
下面为我的代码:
#include<stdio.h>
long long min(long long a,long long b)
{
if(a>b)
{
return b;
}
else
{
return a;
}
}
//取最小值
long long maxgy(long long a,long long b)
{
long long q;
for(long long k=min(a,b);k>=1;k--)
{
if(a%k==0&&b%k==0)
{
q=k;
return q;
}
}
}
//求最大公约数
main()
{
int n;
scanf("%d",&n);
long long a[101],b[101];
int i=0;
while(i<n)
{
scanf("%ld/%ld",&a[i],&b[i]);
i++;
}
for(int j=0;j<i-1;j++)
{
long long q=maxgy(b[j],b[j+1]);
long long B=(b[j]/q)*b[j+1];
long long A=a[j]*(b[j+1]/q)+a[j+1]*(b[j]/q);
long long t=maxgy(A,B);
A=A/t;
B=B/t;
a[j+1]=A;
b[j+1]=B;
}
i--;
b[i]*=n;
long long t=maxgy(a[i],b[i]);
a[i]=a[i]/t;
b[i]=b[i]/t;
if(b[i]==1)
{
printf("%ld",a[i]);
}
else
{
printf("%ld/%ld",a[i],b[i]);
}
}
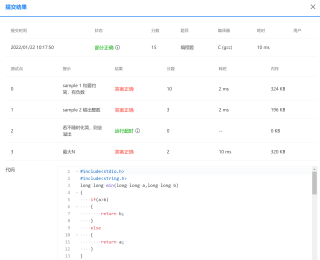
测试用例三显示运行超时;
求各位在我的代码基础上做一些优化并指出我的问题所在(怕看不懂┭┮﹏┭┮)
