基本要求：在一个3×3的九宫格中有1—8这8个数字，混乱排序，一个空格随机地摆放在一个格子里，九宫格布局随机生成。现要求将该九宫格调整为正常按逆序的格式。
调整的规则是：每次只能将与空格（上、下或左、右）相邻的一个数字平移到空格中。
编程求解这一问题，并输出每一步求解过程（坐标：数据：移动方向）。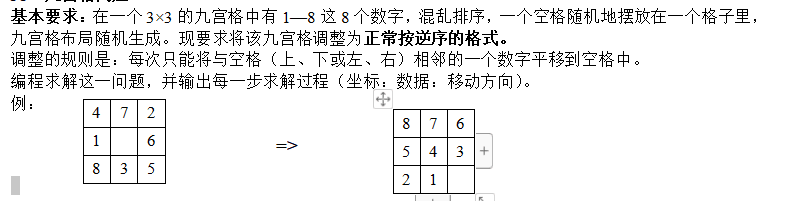
例：
4 7 2 => 8 7 6
1 0 6 => 5 4 3
8 3 5 => 2 1 0
八数码逆序问题求解！！详尽代码解释，小白学习数据结构中！
- 写回答
- 好问题 0 提建议
- 追加酬金
- 关注问题
分享- 邀请回答
-
0条回答 默认 最新
- 2022-11-15 20:46回答 2 已采纳 你把问题想复杂了，可以直接从最后一个元素开始输出，不必交换数组元素，令i=n-1,i>=0时循环输出a[i]，i--。
- 2021-11-28 08:35回答 1 已采纳 供参考： #include<stdio.h> int main() { int a[100],p,q,t,i,n; scanf("%d",&n); for(i=0;
- 2022-11-15 17:05回答 4 已采纳 n1=n2/10改为n1/=10
- 2021-04-11 01:11兔老大RabbitMQ的博客 本文代码实现基本按照《数据结构》课本目录顺序，外加大量的复杂算法实现，一篇文章足够。能换你一个收藏了吧？
- 2022-11-05 23:39回答 1 已采纳 #include<stdio.h> int main() {int n=0,i=0,j,t; int a[10]; scanf("%d",&a[0]); 【先放一个，之后没到-1就一
- 2022-11-09 09:35回答 2 已采纳 scanf("%d",&a); #include<stdio.h> int main() { int a; printf("输入:"); scanf("%d",&a); printf("
- 2021-09-14 07:36回答 3 已采纳 #include <stdio.h> #include <stdlib.h> #include <string.h> void fun(char str[], c
- 2020-01-18 12:22帅地的博客 由于文章有点多，并且发的文章也不是一个系列一个系列发的，不过我的文章大部分都是围绕着 数据结构 + 算法 + 计算机网络 + 操作系统 + Linux + 数据库 这几个方面发的，为了方便大家阅读，我整理了一波。...
- 2022-02-13 15:38回答 5 已采纳 计算w错了，反了。 w=z*100+y*10+x;
- 2021-10-23 17:52回答 1 已采纳 你不得填到15行 /* code */那里吗？？？
- 2022-01-04 21:08回答 1 已采纳 参考代码如下： #define ERROR 0 #define OK 1 #include <stdio.h> #include <stdlib.h> struct CirNo
- 2022-10-17 14:14肩匣与橘的博客 数据结构是计算机科学与技术专业、计算机信息管理与应用专业，电子商务等专业的基础课，是十分重要的核心课程。所有的计算机系统软件和应用软件都要用到各种类型的数据结构。
- 2021-10-31 01:02回答 1 已采纳 输入以为数.在以相反数输出,由于python特性,输入的字符都将以字符串的形式返回,所以,最简洁的方法即是得到字符串后反转字符串,再将其转换为对应类型变量,参考代码如下 a=input('请输入
- 2022-07-14 14:43shejizuopin的博客 语言C++环境：Visual Studio 2019八数码问题是指这样一种游戏：将分别标有数字 1，2，3，…，8 的八块正方形数码牌任意地放在一块 3 * 3 的数码盘上。放牌时要求不能重叠。于是，在 3*3 的数码盘上出现了一个空格。...
- 2019-10-07 22:10Liamcoder的博客 顺序表的基本操作2.1）初始化顺序表2.2）求指定位置元素2.3）插入数据元素2.4）按元素值查找2.5）删除数据元素2.6）顺序表的元素逆置2.7）删除下标为i~j的数据元素2.8）Partition操作3. 单链表的基本操作3.1）初始...
- 2022-10-11 23:34computer初学者的博客 在八数码问题中，棋局的每一个不同的状态都是一个节点，节点之间的转换是通过移动空格实现的。这样，通过选定初始节点和确定图转换规则（本问题中就是移动空格），我们就可以生成一个状态图，如：既然问题已经转化为...
- 2021-04-24 14:38Baret-H的博客 选择排序——堆排序什么是堆堆排序基本思想步骤图解代码实现5. 插入排序——简单插入排序6. 插入排序——希尔排序7. 归并排序8. 基数排序 1. 交换排序——冒泡排序 从要排序序列的第一个元素开始，一次比较相邻...
- 2022-12-25 17:28吉始的博客 排序有内部排序和外部排序，这里八大排序就是内部排序，指直接插入，希尔，选择，堆排，冒泡，快排，归并，计数。 附有动图解释和思维导图汇总
- 2021-03-29 10:21兔老大RabbitMQ的博客 压缩空间 四边形不等式优化 换一种思路 最优解 测试： 第三节 3.1斐波那契之美 3.2桶排序 3.3快速排序 3.4BFPRT 第四节 4.1防止新手错误的神级代码 4.2不用额外空间交换两个变量 4.3八皇后问题神操作 4.4马拉车——...
- 没有解决我的问题, 去提问
悬赏问题
- ¥15 素材场景中光线烘焙后灯光失效
- ¥15 请教一下各位，为什么我这个没有实现模拟点击
- ¥15 执行 virtuoso 命令后，界面没有，cadence 启动不起来
- ¥50 comfyui下连接animatediff节点生成视频质量非常差的原因
- ¥20 有关区间dp的问题求解
- ¥15 多电路系统共用电源的串扰问题
- ¥15 slam rangenet++配置
- ¥15 有没有研究水声通信方面的帮我改俩matlab代码
- ¥15 ubuntu子系统密码忘记
- ¥15 保护模式-系统加载-段寄存器