求助:最近,发现了一种新的数组排序方法,初测其速度是快速排序法的近50倍,想知道有没有市场价值,时间复杂度能计算出来吗?请各位大神赐教!
下面,为了便于区别说明将这个新方法暂且称之占位排序法;
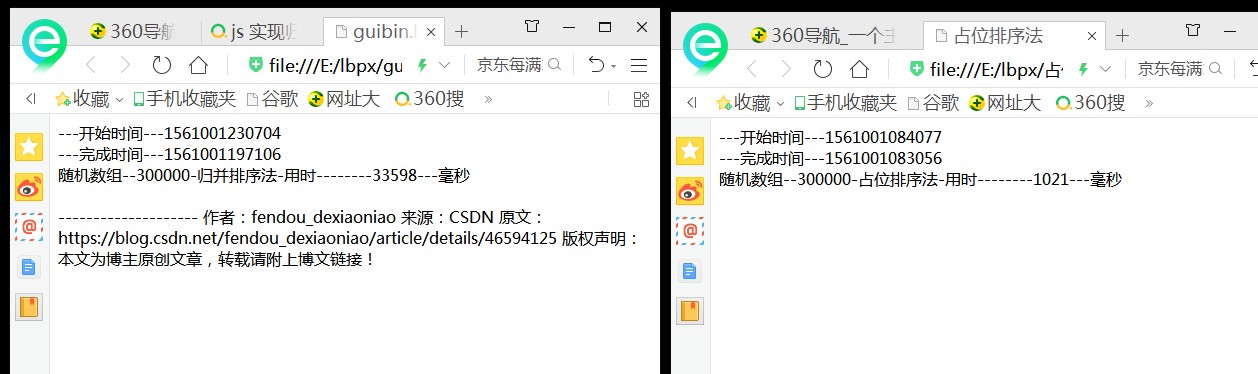
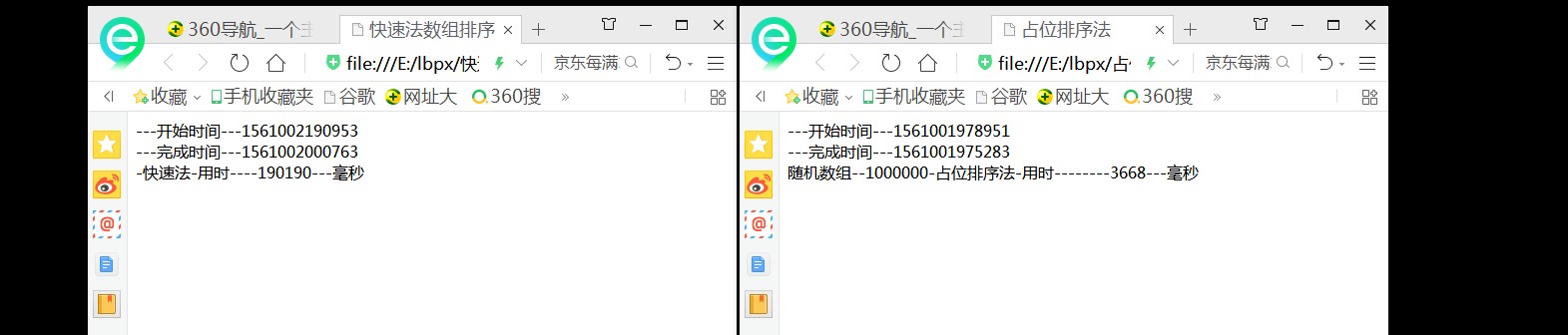
用javascript脚本语言实现快速排序法和占位排序方法之后,然后在同一台(较老旧的,cpu是AMD推土机)电脑上,用ie浏览器运行,样本1000时,快速排序法和占位排序法所耗时分别是:18毫秒、15毫秒;样本10000时,所耗时间分别是:95毫秒、80毫秒;样本100000时,耗时分别是:2405毫秒、407毫秒;样本1000000时,耗时分别是:190888毫秒、3962毫秒;占位方比快排法在对100万数据进行排序时,快了近50倍!!!
占位排序法的理念是:一是,只对数组全局作一次遍历,以后每次只遍历数组的一小部分;二是,把数据的迁移次数降至极致。
占位法的实现方法是:
分段处理、选取代表、萝卜占位、先乱后治、小马快跑、多看少动;
将一个大的数组分割成多个段;首先,要在各段数据p内明确锚点位;其次,锚点位的确定要遵守一个预先明确的固定规范;
其特征还在于,在锚点位上保存的数据不仅要体现自身的数据特征,还要能体现所在段p共同的数据特征。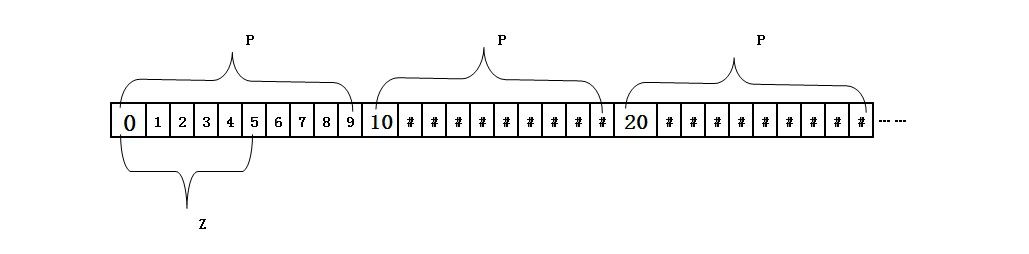
举例:如果在段p内,继续分段p_;假设一个索引地址m; m即是段p的锚点位,又是p_的锚点位,那么在索引m存放的数据,要求必须同时体现:自身的数据征、段p的共同的数据特征、段p_的共同的数据特征;如果对锚点位的数据操作直接作用在需要排序的数据集合上,称之为内建锚点(以下所有实例如无特别说明均采用内建锚点的方式);如果对锚点位的数据进行的操作,还需要额外的映射在另外一个数据集合上,则称之为外建锚点。
列举一个实例,做进一步说明:要从大到小重新排序一个数组A;数组A有100个元素:数据d,规定从A[0]开始每5个数据为一组p_;同时,从A[0]开始每15个数据为一组p;这样一个p内就有3个p_;更进一步,规定每个段的第一个索引对应段的锚点位;那么,A[0]是p的锚点位,又是p_的锚点位;则,A[5]是p_的一个锚点位,而不是p的锚点位;假设初始状态:A[0]存放的数据为5、A[3]为6、A[7]为9、A[12]为8,其他数据均为2;为了在排序过程中,减少遍历和迁移数据的数量,选择最大值来表达每一段数据的共同属性;这样在p_内,A[0]和A[3]的数据值要进行交换;在p内,A[0]和A[7]的数据值还要进行交换,优选的,不仅交换A[0]和A[7]的数据值,还要对A[0]至A[4]与A[5]至A[9],两个p_段内的数据进行整理,使A[0]至A[9]中最大的5个数迁移至A[0]至A[4]中,A[0]至A[9]中最小的5个数迁移至A[5]至A[9]中;最后的结果为:A[0]为9、A[5]为2、A[10]为8。
所述的萝卜占位,指的是“一个萝卜、一个坑”的占位理论在计算机数据整理和筛选过程中的运用;
一方面,更具体的,假设要从一个更大的数据集合中筛选出最小的n个数据,那么只要从数据集合中任意找出n个数据,然后再从这n个数据中找到最大的一个n_,据此就可以准确的进行以下推断:如果存在一个数据大于n_,那么该数据一定不是要选的数据;如果存在一个数据n_1,只要n_1小于n_,那么就又能证明了n_这个数据一定不是要选的,所以就可以安全的用n_1将n_替换掉了;接下来,对调整后的n个数据重新排查,再次找出n个数据中最大的那个,然后重复以上操作,直到将所有符合要求的数据都找出来;
另一方面,设定锚点存放的是每个数据段p的最小的值,p段里面还有p_段,要筛选出最小的n个数据;那么,就可以先遍历p的锚点,选择出锚点值最小的n个p段,再从这n个p段中出找出锚点值最小的n个p_段;再从这n个p_中找到锚点的值最大的p_1;最后遍历这n个p_数据段的数据,只有满足小于或等于p_1,同时又小于n_的值才有可能是要选取的值,所以可以安全的操作这些数据与n_的数据进行互换; 否则,一定不是,所以可以将它们安全的排除在目标之外;
而从一个更大的数据集合中筛选出最大的n个数据,与此逻辑相同,但取值相反;具体的, 只要从数据集合中任意找出n个数据,然后再从这n个数据中找到最小的一个n_,据此就可以准确的进行以下推断:如果存在一个数据小于n_,那么该数据一定不是我们要选的数据;如果存在一个数据n_1,只要n_1大于n_,那么就又能证明了n_这个数据一定不是我们要选的,所以就可以安全的用n_1将n_替换掉了;接下来,对调整后的n个数据重新排查,再次找出n个数据中最小的那个,然后重复以上操作,直到将所有符合要求的数据都找出来;
另一方面,更进一步,接上例,更具体的,设定锚点存放的是每个数据段p的最大的值,p段里面还有p_段,要筛选出最大的n个数据;那么,就可以先遍历p的锚点,选择出锚点值最大的n个p段,再从这n个p段中出找出锚点值最大的n个p_段;再从这n个p_中找到锚点的值最小的p_1;最后遍历这n个p_数据段的数据,只有满足大于或等于p_1,同时又大于n_的值才有可能是要选取的值,所以可以安全的操作这些数据与n_的数据进行互换;否则,一定不是,所以可以将它们安全的排除在目标之外;
通过这种方法有效的减少了数据的遍历数量和数据的交换次数;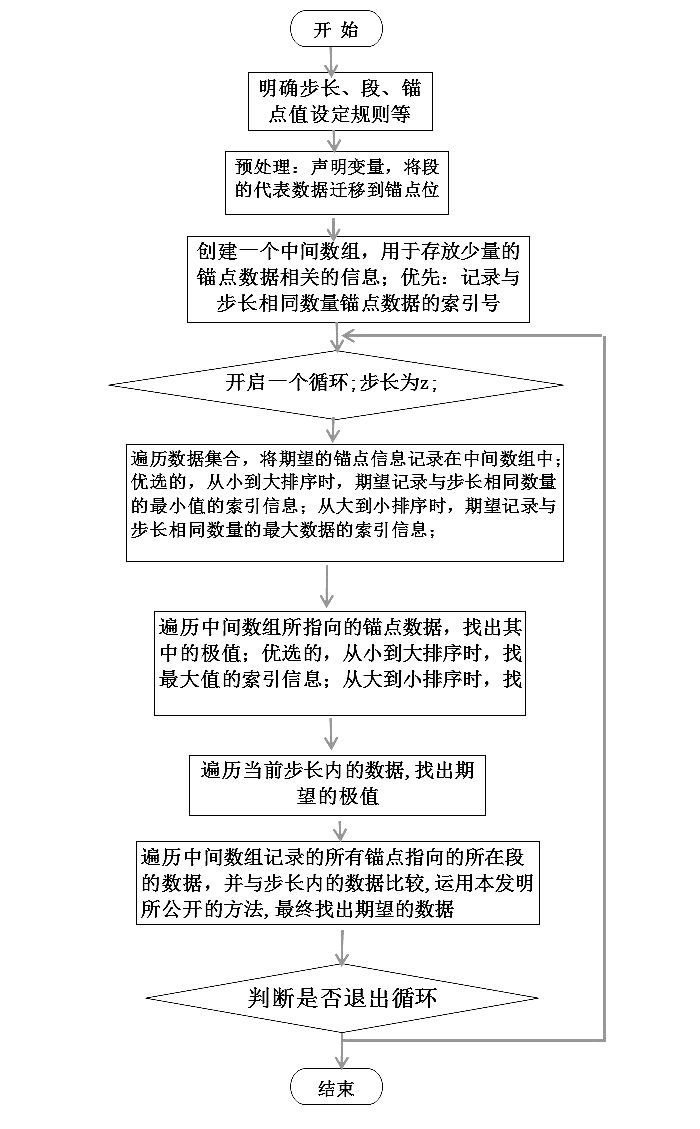
<!doctype html><head><meta charset="UTF-8"><title>占位排序法</title></head><body><script>
/**********用于随机产生一个测试用数组*****/
function arrcf(arr,arrLength){
for(var i = 0; i < arrLength; i++){arr[i]=Math.floor(Math.random()*10000);};}
var arr = new Array(); arrcf(arr,1000000);//调用生成随机数组
var d = new Date(); var t = d.getTime();//记录程序开始的
/**********用于随机产生一个测试用数组****/
var z =25; //步长,每次可排好的数据个数,可调整
var p =4*z; //数据分段长度,可根据实际情况调整
var pxb = 0; //prr数组中arr[prr[*]]最大值的下标*
var pxm = 0; //arr[prr[*]]中最小值的下标*
var f2 = arr.length; //数组长度
var fi = f2-z; //段的头部
var mx = fi; //步长内极值(最小值)的下标
var pi = 0; //中间过渡变量
var prr = new Array();//中间过渡数组
/**** 预处理 ***************/
ycl(f2);
/**** 全面排序 *************/
for(var fi=f2-z;fi>0;fi-=z){
//向prr[]填充z个p节点的下标
var prr= new Array();
for (var iii=0;iii<z;iii++ ){ prr[iii]=iii*p;}
//找出arr[prr[*]]最小的*值
pxb = prrmax(pxb);
//便历节点找出最大的z个数据,更新prr[]
for(var ii=(z)*p; ii< fi ;ii+= p){
if(arr[prr[pxb]]<arr[ii]){ prr[pxb]=ii;
//重新确定prr[]中的最小值
pxb = prrmax(pxb);}}
mx=colt(z,fi); //获取步长内的最小值
//遍历prr数组
for(var i=0;i<z;i++){ pi=prr[i];
if(arr[mx]<arr[prr[i]]){ //步长内的最小值,是否小于段的最大值
var z1= Math.floor(fi/p)*p;
if(z1===pi){ //判断步长的头部是否在段内
//处理尾部数据,即步长头部所在的段
var z1= Math.floor(fi/p)*p;
for(var ii=z1;ii<fi;ii++){ //遍历arr[]数组的当前段
if(arr[ii] >= arr[prr[pxb]]){ //如果当前值不小于arr[prr[]]最小值
if(arr[ii]>arr[mx]){
dtod(ii,mx);
mx=colt(z,fi); //获取步长内的最小值
}}
if(arr[ii]>arr[pi]){ //动态维护本段的最大值
pi=ii;
}}
//保存最大值到段的开头位置
if(arr[pi]>arr[prr[i]]){dtod(pi,prr[i]);}
}else{
for(var ii=prr[i];ii<prr[i]+p;ii++){ //遍历arr[]数组的当前段
if(arr[ii] >= arr[prr[pxb]]){ //如果当前值大于等于prr[]中的arr[prr[]]最小值
if(arr[ii]>arr[mx]){ //如果当前值大于数组中的最小值
dtod(mx,ii); //数据交换
mx=colt(z,fi); //重新获取步长内的最小值
}}
if(arr[ii]>arr[pi]){ //动态维护本段的最大值
pi=ii;
}}
//保存最大值到段的开头位置
if(arr[pi]>arr[prr[i]]){
dtod(pi,prr[i]);
}}}}
if(fi>p*z){
var fz=fi;
var zf=fi+z;
zpx(fz,zf);
}else{
var fz=0;
var zf=fi+z;
zpx(fz,zf);
break;
}}
/************以下位置用于封装函数*****************************/
//标记段数据的最大值属性
function ycl(f2){
for (var i=0;i<f2;i += p ){
var max=i;
var rp=i+p;
for(var ii=i;ii<rp;ii++){
if(arr[max]<arr[ii]){
max=ii;
}}
dtod(i,max);
}}
//选取步长内最小数据的索引号
function colt(z,fi){var mrx=fi+z;
for(var i=fi;i<mrx;i++){if(arr[mx]>arr[i]){mx=i;}}return(mx);
}
//数据交换
function dtod(dt1,dt2){y=arr[dt1];arr[dt1]=arr[dt2];arr[dt2]=y;}
//找出arr[prr[i]]最小的i值
function prrmax(pxb){
var pxb=0;
for(var pi = 0;pi<z;pi++){if(arr[prr[pxb]]>arr[prr[pi]]){pxb=pi;}}return(pxb);}
//以1为步长,双向式,对数据排序
function zpx(fz,zf){ //zf排序的开始位置,fz排序的结束位置
for(fz;fz<zf;zf){
var mi=fz; //记录最小值
var ma=zf-1; //记录最大值
if(arr[fz]>arr[zf-1]){dtod(fz,zf-1);}//前后两个数比较,交换位置
for(var i=fz;i<zf;i++){
if(arr[i]<arr[mi]){mi=i;}else if(arr[i]>arr[ma]){
ma=i;
}}
dtod(fz,mi);
dtod(ma,zf-1);
fz++;
zf--;
}}
/**********以下用于输出结果**********************/
//for(var i=0;i<arr.length;i++){ document.write(arr[i]+",,,,,"+i+"<br>")};
var t2=(new Date().valueOf());document.write("---开始时间---"+t2+"<br>---完成时间---"+t+"<br>-占位排序法-用时--------"+(t2-t)+"---毫秒<br>");
for(var i=0;i<arr.length;i++){if(arr[i-1]>arr[i]){alert("数组排序有误,错误在:"+i);}else{x1=-1;}};if(x1<0){alert("排序正确");};
</script></body></html>
```下面是快排法
<!doctype html><head><meta charset="UTF-8">
<title>快速法数组排序</title></head><body>
<script>
//用于随机产生一个测试用数组
function arrcf(arr,arrLength){ //数组名字(调用前在函数外声明一下,做在全局的),数组长度
for(var i = 0; i < arrLength; i++){arr[i]=Math.floor(Math.random()*1000);};
}
//调用生成随机数组
var arr = new Array(); arrcf(arr,1000000);
var d = new Date(); var t = d.getTime();//记录程序开始的时间,用于测试程序执行效率
/********* (以下代码采用52.0Hz的方案,https://blog.csdn.net/Loving_M/article/details/52993521)******/
var times=0; var quickSort=function(arr){
//如果数组长度小于等于1无需判断直接返回即可
if(arr.length<=1){return arr;}
var midIndex=Math.floor(arr.length/2);//取基准点
var midIndexVal=arr.splice(midIndex,1);//取基准点的值,splice(index,1)函数可以返回数组中被删除的那个数arr[index+1]
var left=[];//存放比基准点小的数组
var right=[];//存放比基准点大的数组
//遍历数组,进行判断分配
for(var i=0;i<arr.length;i++){
if(arr[i]<midIndexVal){left.push(arr[i]);}//比基准点小的放在左边数组
else{right.push(arr[i]);}//比基准点大的放在右边数组
}
//递归执行以上操作,对左右两个数组进行操作,直到数组长度为<=1;
return quickSort(left).concat(midIndexVal,quickSort(right));
};
quickSort(arr);
/*******************************************************************************************/
//用于输出结果
var t2=(new Date().valueOf()); document.write("---开始时间---"+ t2 +"<br>---完成时间---"+t+"<br>-快速法-用时----"+(t2-t)+"---毫秒<br>");
</script></body></html>