知道一组离散点坐标，根据垂距法用matlab提取出特征点

Question

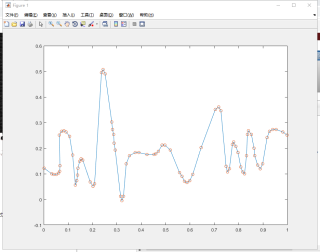
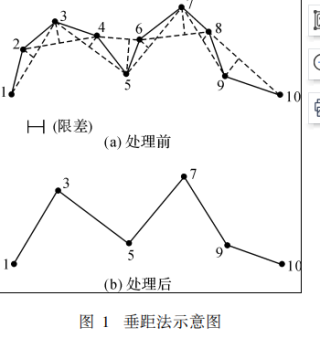
用垂距法解，垂距法是指根据中间顶点到其前、后两 相邻顶点连线的距离的大小，来确定是否保留该顶点的一种线要素顶点压缩算法。当求得的距离大于给定的限差（阈值）时，保留该顶点，否则删除该 顶点。该算法在实施过程中，首先按顶点的顺序将 相邻的三个固定顶点组成一系列三元组，然后顺次取一个三元组进行处理，直至所有的三元组处理完毕为止。（如图 １所示）。

我的具体想法是：首先用直线两点式公式(y-y2)/(y1-y2) = (x-x2)/(x1-x2)求出第一与第三个点连线的公式，整理成标准形式Ax +By+C =0。再用点到直线的距离公式d =fabs(A x +B y +C) /sqrt(AA +BB)求出第二个点到直线的距离，若大于某个值a则保留第二个点，以此类推。
当y1=y2或x1=x2的话就用y=y1或x=x1算；阈值可以取所有点到直线距离的中位数
（附离散点坐标）
0.00149868 0.121951
0.0123244 0.114634
0.0219453 0.107317
0.0327711 0.1
0.0411989 0.097561
0.0520423 0.097561
0.0604878 0.102439
0.0653247 0.109756
0.0665824 0.131707
0.0648634 0.168293
0.0637173 0.192683
0.0631854 0.221951
0.0638584 0.25122
0.0729298 0.265854
0.0825742 0.268293
0.0915986 0.263415
0.0994064 0.253659
0.106015 0.246341
0.110793 0.229268
0.114952 0.204878
0.11849 0.173171
0.119618 0.141463
0.121963 0.114634
0.123688 0.0804878
0.125472 0.0707317
0.129653 0.0560976
0.135116 0.0731707
0.138783 0.095122
0.140053 0.121951
0.143708 0.139024
0.147346 0.14878
0.153394 0.158537
0.160009 0.153659
0.165401 0.141463
0.170782 0.12439
0.177361 0.104878
0.183941 0.0853659
0.190526 0.0682927
0.196527 0.0585366
0.201931 0.0512195
0.208581 0.0609756
0.212845 0.0804878
0.215915 0.104878
0.218413 0.141463
0.220291 0.170732
0.221584 0.207317
0.223479 0.243902
0.225386 0.285366
0.22727 0.317073
0.22854 0.343902
0.230441 0.382927
0.231728 0.417073
0.233003 0.446341
0.234881 0.47561
0.236735 0.495122
0.243391 0.507317
0.251784 0.490244
0.255351 0.470732
0.260106 0.443902
0.263053 0.417073
0.266609 0.392683
0.269539 0.358537
0.274282 0.326829
0.279042 0.302439
0.281984 0.273171
0.286756 0.253659
0.288481 0.219512
0.293235 0.192683
0.296165 0.158537
0.299101 0.126829
0.303247 0.097561
0.307393 0.0682927
0.310932 0.0365854
0.31509 0.0121951
0.32047 -0.00487805
0.327138 0.0121951
0.329624 0.0439024
0.332116 0.0780488
0.335228 0.119512
0.338287 0.139024
0.342533 0.15122
0.351616 0.170732
0.363682 0.178049
0.37514 0.182927
0.3902 0.182927
0.400435 0.180488
0.411272 0.178049
0.423315 0.17561
0.435965 0.17561
0.443194 0.17561
0.45223 0.17561
0.459465 0.178049
0.470332 0.187805
0.485451 0.212195
0.496897 0.212195
0.509524 0.202439
0.519139 0.192683
0.527532 0.17561
0.535316 0.156098
0.547299 0.129268
0.556879 0.104878
0.567085 0.0902439
0.577279 0.0707317
0.587508 0.0658537
0.598971 0.0731707
0.611078 0.097561
0.622607 0.131707
0.636562 0.173171
0.645669 0.202439
0.655366 0.226829
0.666882 0.256098
0.678398 0.285366
0.688096 0.309756
0.695974 0.329268
0.703858 0.35122
0.717737 0.360976
0.726738 0.346341
0.731481 0.314634
0.736189 0.268293
0.73851 0.231707
0.74144 0.197561
0.744376 0.165854
0.747902 0.129268
0.753873 0.107317
0.761734 0.119512
0.766039 0.156098
0.770332 0.187805
0.774011 0.214634
0.778854 0.22439
0.787849 0.207317
0.796826 0.182927
0.803382 0.153659
0.808137 0.126829
0.815921 0.107317
0.823735 0.1
0.828058 0.143902
0.831737 0.170732
0.833656 0.217073
0.835551 0.253659
0.839803 0.268293
0.851816 0.253659
0.856565 0.22439
0.86253 0.2
0.865472 0.170732
0.871449 0.15122
0.877432 0.134146
0.88824 0.119512
0.897925 0.139024
0.902827 0.173171
0.908325 0.204878
0.916244 0.241463
0.925942 0.265854
0.939212 0.273171
0.953068 0.273171
0.969321 0.268293
0.980755 0.263415
0.998196 0.25122

Answer 1

points=load('1.txt');
count=2;
ps(1,:)=points(1,:);%添加第一个点到结果（第一个点必然在）
l=length(points);
for i = 2:l-1%（遍历中间的所有点）
    x1=points(i-1,1);
    x0=points(i,1);
    x2=points(i+1,1);
    y1=points(i-1,2);
    y0=points(i,2);
    y2=points(i+1,2);
    d(i) = (abs((y2 - y1) * x0 +(x1 - x2) * y0 + ((x2 * y1) -(x1 * y2)))) / (sqrt((y2 - y1)^2 + (x1 - x2)^2));
    %计算每个垂距
    
end
th=d(round(l/2));%取中位数位阈值
for i =2:l-1
   if d(i)>th%如果垂距大于阈值则添加点
      ps(count,:)=points(i,:); 
      count=count+1;
   end
end
ps(count,:)=points(l,:);%添加最后一个点到结果（最后一个点必然在）
plot(ps(:,1),ps(:,2));
hold on;
scatter(ps(:,1),ps(:,2))