请问如何用matlab找到大于10^15的最小正整数n，这个n要同时满足2n+1和3n+1是平方数？

Question

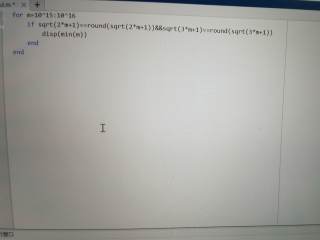
请问如何用matlab找到大于10^15的最小正整数n，这个n要同时满足2n+1和3n+1是平方数？（举个例子，3960就满足这个性质，2x3960+1=89^2，3x3960+1=109^2）如图，我目前想到的是大致确定n的范围（乱定的），导致速度缓慢，无法求解。

Answer 1

历时 1.810428 秒，计算完毕！

代码如下：

clear all
clc
format long

tic
% 确定平方数的范围
a = round(sqrt(2*(1e+15)+1));
b = round(sqrt(3*(1e+16)+1));

len = b-a;
nums1 = zeros(len,1);
nums2 = zeros(len,1);

% 穷举由平方数经过变换后产生在10^15-10^16之间的数
j = 1;
for i = a:b
    nums1(j)=(i^2-1)/2;
    nums2(j)=(i^2-1)/3;
    j = j+1;
end

% 找出两个数组中第一个相同的数，就是满足条件的最小整数
i = 1; j=1;
while(i<=len&&j<=len)
    if(nums1(i)==nums2(j))
        disp(['满足条件的最小整数为：' num2str(nums1(i))]);
        break;
    end
    if(nums1(i)<nums2(j))
        i = i +1;
    else
        j = j + 1;
    end
end
toc