我在做蓝桥杯 印章练习题时,在所有可能的输出数据都一样的情况下,别人的是测评结果是正确,然而我的却显示错误,只有87分,(!重点:输出数据完全一样!)
题目:
共有n种图案的印章,每种图案的出现概率相同。小A买了m张印章,求小A集齐n种印章的概率。
输入格式
一行两个正整数n和m
输出格式
一个实数P表示答案,保留4位小数。
样例输入
2 3
样例输出
0.7500
数据规模和约定
1≤n,m≤20
我的思路:
两个变量,应用二维数组,设dp[i][j]表示买 i 张集齐 j 种的概率。(注意不是刚好集齐 j 种);每一次买中任何一种的概率都是1/n;
第一步:确定状态
最后一步:已经买了m-1张了,正在买这最后一张,由于除了买第一张外其他时候都有可能出现买到重复的和不是重复的两种情况,所以此时的最后一步有两种情况:
1、前面的m-1张早已经集齐n种了,最后一张只是在买一个已经有了的种类而已
概率 dp[m][n] = dp[m-1][n] * 1;
2、前面的m-1张已经集齐n-1种,而正在买的这最后一张刚好是差的那最后一种
概率 dp[m][n] = dp[m-1][n-1]*1/n;
化子问题:
1、目前正在买第 i (i<m)张,设前面的 i-1 张早已经集齐 j (j<n)种,而刚买的这张恰巧是这 j 种中的一种,买中的概率为 j/n;则有 dp[i][j] = dp[i-1][j] * j/n;
2、目前正在买第 i (i<m)张,设前面的 i-1 张刚好集齐 j-1 (j<n)种,而刚买的这张刚好是还没有集齐的 n - (j-1) 种中的一种,买到概率为 (n-j)/n;即有 dp[i][j] = dp[i-1][j-1] *(n-j+1)/n;
第二步:状态转移
dp[i][j] = dp[i-1][j] * j/n + dp[i-1][j-1] *(n-j+1)/n;
第三步:初始条件和边界情况
初始条件:当 i<j 时 ,dp[i][j]=0;(买的张数都小于种类数了集齐的概率当然为 0 咯),所以初始条件必须是i>=j的情况下此方程才可行。
边界情况:dp[0][0]=1;
第四步:计算顺序
从已知向未知方向出发,已知dp[1][1]=1;未知dp[m][n],所以for循环顺序是1到m和1到n;
我的代码:
#include<iostream>
#include<cmath>
using namespace std;
double dp[21][21];
int main(){
int n,m;
cin>>n>>m;
if(m<n)
dp[m][n]=0.0;
else{
dp[0][0]=1.0;
for(int i=1; i<=m; i++)
{
for(int j=1; j<=n; j++)
{
if(i<j)
dp[i][j]=0.0;
else
dp[i][j] = dp[i-1][j]*(j*1.0/n) + dp[i-1][j-1]*((n-j+1)*1.0/n);
}
}
printf("%.4f\n",dp[m][n]);
}
return 0;
}
测评结果错误
下面是别人的完全正确的代码
#include <iostream>
#include <cmath>
using namespace std;
double dp[25][25], p;
int main()
{
int n, m;
cin >> n >> m;
p = 1.0 / n;
for ( int i = 1; i <= m; ++i ) {
for ( int j = 1; j <= n; ++j ) {
if ( i < j ) dp[i][j] = 0;
if ( j == 1 ) {
dp[i][j] = pow (p, i-1); //p^(i-1)
}
else {
dp[i][j] = dp[i-1][j] * (j*1.0/n) + dp[i-1][j-1] * ((n-j+1)*1.0/n);
}
}
}
printf("%.4lf ",dp[m][n]);
return 0;
}
然后我用下面的代码对比了两个版本对应数据,输出对应不同的数据:
#include<iostream>
#include<cmath>
using namespace std;
double dp[21][21];
double dp1[25][25], p;
int main(){ //以下是所有数据对比
int main1();//100分的
int main2();//87分的
main1();
main2();
for(int i=1; i<=20; i++)
for(int j=1; j<=20; j++){
if(dp[i][j]!=dp1[i][j])
//只要对应数据不同就输出来
printf("%d %d %.15lf %.15lf\n",j,i,dp[i][j],dp1[i][j]);
}
return 0;
}
函数略
输出的结果居然是:
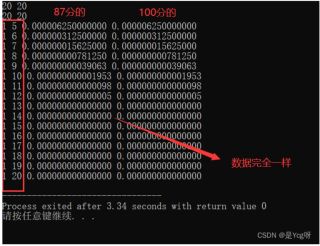
这是为什么呀?
