matlab中调用函数用fplot绘制不出来曲线

Question

问：matlab中明明调用了fplot函数绘制出来的图形还是直线而不是曲线，试了好多次还是不行

代码

clear 
clc

%A=700;beta=0.000000053;mu=0.001;delta1=0.020;delta2=0.010;psi=0.5;sigma=0.85;gamma=0.8;
% s=10;   d=0.01;  r=0.1; beta=0.00015; c=0.1;  alpha=1; gama=1; q=0.1; m=0.3; delta=1;

 s=10;   d=0.01;  p=0.1; beta=0.00015; elta=1;  b=0.25;  c=1;  m=0.05; k1=0.000135; delta=0.1; k2=0.000135;
%s=10;   d=0.01;  p=0.1; beta=0.00015; elta=1;  b=0.01;  c=2 ; m=1; k1=0.000135; delta=0.1; k2=0.00015;

 v1=m+b.*elta-c;
 u1=4.*b.*m.*elta;
 Delta1=v1^2-4.*u1;
c1=roundn(b.*elta+m+2.*sqrt(m.*elta.*b),-10); 
 Q=8.8*((-exp(-10000)+0.5.*exp(0.25-20000))-(-exp(-0.25)+0.5.*exp(0.25-0.5)));
 R0=(s.*(k1+k2.*Q))./(d.*delta);
 T1=s./(d.*R0);
 I1=(d.*(R0-1))./beta;
 L1=k2.*T1.*I1;

 c2=roundn(m+b.*elta+m.*elta.*d.*(R0-1)./beta+b.*beta./(d.*(R0-1)),-10);
 I_=(c-m-(b.*elta)-sqrt((b.*elta+m-c)^2-(4.*m.*elta.*b)))./(2.*m.*elta);
 I__=(c-m-b.*elta+sqrt((b.*elta+m-c)^2-4.*m.*elta.*b))./(2.*m.*elta);
 T_=s./(d+beta.*I_);
 E_=(T_.*(k1+k2.*Q)-delta)./p;
 T__=s./(d+beta.*I__);
 E__=(T__.*(k1+k2.*Q)-delta)./p;
 L2=k2.*T_.*I_;
 Rc=1+(beta.*sqrt(b./(m.*elta)))./d;
 R21=s.*(k1+k2.*Q)./(delta.*(d+beta.*I_));
 R11=s.*(k1+k2.*Q)./(delta.*(d+beta.*I__));
 

f1p=@(c) (-(m+b.*elta-c)+((m+b.*elta-c)^2-4.*b.*m.*elta)^0.5)./(2.*m.*elta);
f1n=@(c) (-(m+b.*elta-c)-((m+b.*elta-c)^2-4.*b.*m.*elta)^0.5)./(2.*m.*elta);

 %f1p = @(c) (-(m+b.*elta-c)+((m+b.*elta-c)^2-4.*b.*m.*elta)^0.5)./(2.*m.*elta);
%f1n = @(c) (-(m+b.*elta-c)-((m+b.*elta-c)^2-4.*b.*m.*elta)^0.5)./(2.*m.*elta);


fplot(f1p,[0,c2],'ShowPoles','off','linewidth',2,'linestyle',':','Color','[0.69,0.09,0.12]');%涓嶇ǔ瀹氱殑姝ｅ钩琛＄偣Q3
hold on
fplot(f1n,[c1,28],'ShowPoles','off','linewidth',2,'linestyle','-','Color','[1,0.6,0.07]');%绋冲畾鐨勬骞宠　鐐筈3
hold on

line([0.03,c2],[I1,I1],'linestyle','-','color','b','linewidth',2);
hold on
line([c2,28],[I1,I1],'linestyle','--','color','r','linewidth',2);
hold on
line([c1,c1],[-1,sqrt(b./(m.*elta))],'linestyle','--','color','k','linewidth',0.2);
hold on

line([c2,c2],[-1,I1],'linestyle','--','color','k','linewidth',0.2);
hold on

xlim ([0.03 28]);

  text(0.03, 500,'\bf (I)')
   ylim([-10,400])
  box on
  text(c1, -12,'c_1')
   text(c2, -12,'c_2')

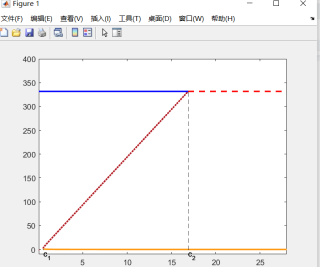
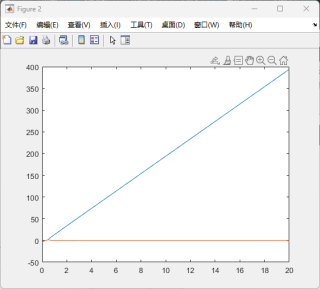
得到的结果：

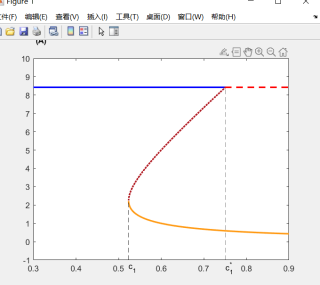
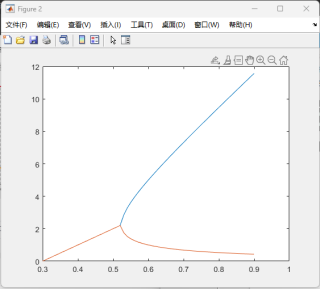
我想要达到的结果：（类似这种）

Answer 1

直接画函数的数值计算后的图，可以看出在[0,20]区间上的函数就是图一这个样子的

c=0:0.01:20;
tf1p=(-(m+b.*elta-c)+((m+b.*elta-c).^2-4.*b.*m.*elta).^0.5)./(2.*m.*elta);
tf1n=(-(m+b.*elta-c)-((m+b.*elta-c).^2-4.*b.*m.*elta).^0.5)./(2.*m.*elta);
figure(2)
plot(c,tf1p)
hold on
plot(c,tf1n)

不过，注意到图二的横坐标范围是[0.3,0.9]，所以可以再画一下这个范围的图对照一下

c=0.3:0.01:0.9;
tf1p=(-(m+b.*elta-c)+((m+b.*elta-c).^2-4.*b.*m.*elta).^0.5)./(2.*m.*elta);
tf1n=(-(m+b.*elta-c)-((m+b.*elta-c).^2-4.*b.*m.*elta).^0.5)./(2.*m.*elta);
figure(2)
plot(c,tf1p)
hold on
plot(c,tf1n)

可以看到，在这个范围内是有题主期望的函数的样子的，看回代码，可以发现两个函数可以简化为一个线性函数加/减一个指数函数，因此可以推测，指数较小，因此只在数值较小时特性明显，当数值较大时，线性函数表现更加明显