如何将高维随机事件的概率转化为一维随机变量随机事件的概率？

Question

请问一般如何将高维随机事件的概率转化为一维随机变量随机事件的概率？可以举一个相对应的例子吗？

Answer 1

方案来自 梦想橡皮擦 狂飙组基于 GPT 编写的 “程秘”

---

在概率论中，可以通过边缘概率分布和条件概率分布的计算，将高维随机事件的概率转化为一维随机变量随机事件的概率。

例如，假设有一个二维随机变量 $(X,Y)$，其概率密度函数为 $f_{X,Y}(x,y)$，现在我们要计算 $X$ 取值在区间 $[a,b]$ 内的概率 $P(a\le X\le b)$，可以使用边缘概率分布计算：

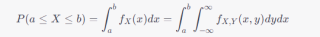
其中 $f_X(x)$ 表示 $X$ 的边缘概率密度函数，可以通过二维随机变量的联合概率密度函数 $f_{X,Y}(x,y)$ 计算得出。类似的，如果要计算 $Y$ 取值在区间 $[c,d]$ 内的概率 $P(c\le Y\le d)$，也可以使用边缘概率分布计算：

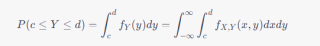
此外，还可以使用条件概率分布来计算一维随机变量随机事件的概率。例如，假设我们要计算在 $Y=y$ 的条件下 $X$ 取值在区间 $[a,b]$ 内的概率 $P(a\le X\le b|Y=y)$，可以使用条件概率分布计算：

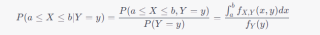
这里 $f_Y(y)$ 表示 $Y$ 的边缘概率密度函数。

总之，通过边缘概率分布和条件概率分布的计算，可以将高维随机事件的概率转化为一维随机变量随机事件的概率。