运用四阶龙格库塔求解得到微分方程组的离散数值解y(t),现在需要在matlab中实现对y(t)做离散时间傅里叶变换求出y*(Ω)的代码,其计算定义如图所示。
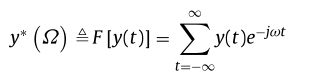
运用四阶龙格库塔求解得到微分方程组的离散数值解y(t),现在需要在matlab中实现对y(t)做离散时间傅里叶变换求出y*(Ω)的代码,其计算定义如图所示。
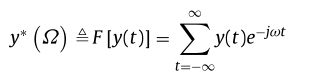
基于Monster 组和GPT的调写:
下面是matlab代码示例,假设y(n)保存在向量y中,N为向量长度,Δt为时间步长:
% 计算DFT
Y = fft(y);
% 频移操作
Yshift = fftshift(Y);
% 计算频率向量
N = length(y);
fs = 1 / (N * Δt); % 采样频率
fnyquist = fs / 2; % 奈奎斯特频率
freq = linspace(-fnyquist, fnyquist, N);
% 计算离散时间傅里叶变换
y_star = Yshift;
其中,linspace函数用于生成频率向量,fft函数用于计算DFT。注意,如果要对y*(Ω)进行可视化,一般需要对结果进行幅值归一化,即y*(Ω)除以N,以便于比较不同信号的能量。