八数码难题，C++蒟蒻来问~

Question

八数码难题
题目描述:
在3×3的棋盘上，摆有八个棋子，每个棋子上标有1至8的某一数字。棋盘中留有一个空格，空格用0来表示。空格周围的棋子可以移到空格中。要求解的问题是：给出一种初始布局（初始状态）和目标布局（目标状态），找到一种最少步骤的移动方法，实现从初始布局到目标布局的转变。

输入格式:
包含六行，每行三个数字，数字之间用空格间隔。前三行为初始状态，后三行为目标状态。
输出格式:
只有一行，该行只有一个数字，表示从初始状态到目标状态需要的最少移动次数。如果无法从初始状态得到目标状态，或移动步数超过25还不能得到目标状态，则输出“No solution!”。
样例输入:
2 8 3
1 6 4
7 0 5
1 2 3
8 0 4
7 6 5
样例输出:
5
题目传送门
神犇们，这一题八数码该咋写……

Answer 1

“Devil组”引证GPT后的撰写：
八数码问题可以使用广度优先搜索（BFS）来解决。具体思路如下：

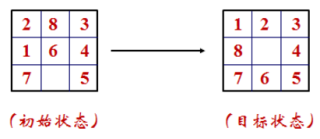
• 将初始状态和目标状态分别表示为一个 3x3 的矩阵，用二维数组来存储。

• 定义状态的结构体，包含当前状态的矩阵、父状态的指针、空格的位置、当前状态的步数。

• 定义队列，将初始状态作为队首入队。

• 对队首进行扩展，即对空格周围的数字进行移动，每一次移动生成一个新的状态，将其存入队列中，同时将当前状态作为新状态的父状态。

• 当队列不为空时，取出队首状态进行扩展，重复步骤 4。

• 直到队列为空，或者找到目标状态，停止搜索。

• 如果找到目标状态，可以从目标状态开始，沿着父状态的指针一直回溯到初始状态，记录每一个状态的步数，即可得到从初始状态到目标状态的最少步数。

c++：

#include <bits/stdc++.h>
using namespace std;
struct node{
    int a[3][3],x,y,g,h;
    bool operator<(const node& p)const{
        return p.g+p.h<g+h;
    }
}cur,nxt;
int tx[4]={1,-1,0,0};
int ty[4]={0,0,1,-1};
priority_queue<node>q;
map<vector<int>,bool>m;
vector<int>v;
int ans[3][3],step=0;
bool check(){
    int cnt=0;
    for(int i=0;i<3;i++){
        for(int j=0;j<3;j++){
            if(cur.a[i][j]!=ans[i][j]){
                cnt++;
            }
        }
    }
    return cnt==0;
}
void Astar(){
    while(!q.empty()){
        cur=q.top();
        q.pop();
        if(check()){
            printf("%d\n",cur.g);
            return;
        }
        for(int i=0;i<4;i++){
            int dx=cur.x+tx[i];
            int dy=cur.y+ty[i];
            if(dx>=0&&dx<3&&dy>=0&&dy<3){
                nxt=cur;
                swap(nxt.a[cur.x][cur.y],nxt.a[dx][dy]);
                nxt.x=dx,nxt.y=dy;
                v.clear();
                for(int i=0;i<3;i++){
                    for(int j=0;j<3;j++){
                        v.push_back(nxt.a[i][j]);
                    }
                }
                if(m[v]){
                    continue;
                }
                nxt.g=cur.g+1;
                nxt.h=0;
                for(int i=0;i<3;i++){
                    for(int j=0;j<3;j++){
                        if(nxt.a[i][j]==0){
                            continue;
                        }
                        nxt.h+=abs(i-(nxt.a[i][j]-1)/3)+abs(j-(nxt.a[i][j]-1)%3);
                    }
                }
                q.push(nxt);
                m[v]=1;
            }
        }
    }
    puts("No solution!");
    return;
}
int main(){
    for(int i=0;i<3;i++){
        for(int j=0;j<3;j++){
            scanf("%d",&cur.a[i][j]);
            if(cur.a[i][j]==0){
                cur.x=i,cur.y=j;
            }
        }
    }
    for(int i=0;i<3;i++){
        for(int j=0;j<3;j++){
            scanf("%d",&ans[i][j]);
        }
    }
    cur.g=0,cur.h=0;
    for(int i=0;i<3;i++){
        for(int j=0;j<3;j++){
            if(cur.a[i][j]==0){
                continue;
            }
            cur.h+=abs(i-(cur.a[i][j]-1)/3)+abs(j-(cur.a[i][j]-1)%3);
        }
    }
    q.push(cur);
    m[v]=1;
    Astar();
    return 0;
}