有一个关于Dijkstra的无向图算法的实现,队列的处理简单,使算法的时间复杂度为𝛩(𝑛2),n是图中的节点数,将该算法应用于无向算法,下面是最初使用的加权图
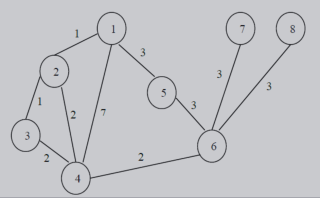
修改算法以解决下列问题:
在一个链路网络中,有n个基站,我们可以在它们之间传输消息,一个网络包含n个互相传输信息的站点t1, t2, …, tn,由于干扰,消息可能在传输过程中被损坏。对于每一对站点,我们都知道消息被正确传输的概率(一个在0到1之间的实数)。 我们打算从t1站到tn站。设计一种算法来找到站点的路径,以最佳的概率传递消息.请注意,当一个消息通过一系列站点传输时,没有错误地传递它的概率是序列中概率的乘积。
例子,在下图中,有三个站点和给定的概率
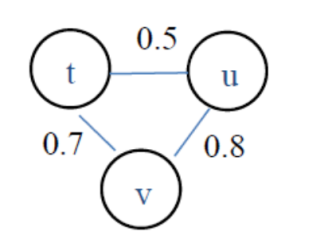
通过v从t向u传递信息比直接传递信息更好,因为直接传递信息概率为0.5,而通过v的概率为0.7 × 0.8 = 0.56 > 0.50
因此,应该修改给定的算法而不是边的和。我们考虑乘积,并选择最大值(而不是像原始算法中那样的最小值)
将该算法应用于以下网络,其中边的权值为概率。该消息将从站1传送到站8,以此图用作新的算法。
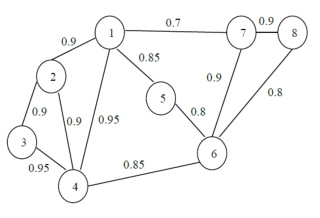
dijkstra.不需要修改
// DSA Programming task 4.2 - Dijkstra
// You do not need to change anything here
#ifndef DIJKSTRA_H_INCLUDED
#define DIJKSTRA_H_INCLUDED
#include <limits.h>
#include <float.h>
// Maximum number of vertices
// define according to your needs
#define MAXVERTS 1000
// Nodes are numbered as integers from 1
// Maximum value in the distance table
#define INF DBL_MAX
// Defines edge in the adjacency list
typedef struct weightedgnd {
int nodenum;
double weight;
struct weightedgnd* next;
} weightededgenode, *pweightededgenode;
// Defines the graph
typedef struct weightedg {
pweightededgenode adj_list[MAXVERTS+1];
int pred[MAXVERTS+1];
double dist[MAXVERTS+1];
int nVertices;
} weightedgraph;
// Initializes graph for breadth-first search
void init_graph(weightedgraph* g, int vertices);
// Adds new edge (x,y)
void add_edge(weightedgraph* g, int x, int y, double wght);
// Actual breadth-first search from node s
void dijkstra(weightedgraph* g, int s);
// Frees allocated memory
void delete_graph(weightedgraph* g, int vertices);
// Print a path after search
void print_path(weightedgraph* g, int dest);
#endif
main.c,不需要修改
// DSA Programming task 4.2 - Dijkstra
// You do not need to change anything here
#include <stdio.h>
#include "dijkstra.h"
int main(){
weightedgraph g;
init_graph(&g,8);
add_edge(&g,1,2,1);
add_edge(&g,1,4,7);
add_edge(&g,1,5,3);
add_edge(&g,2,3,1);
add_edge(&g,3,4,2);
add_edge(&g,5,6,3);
add_edge(&g,6,7,3);
add_edge(&g,6,8,3);
// The other graph
add_edge(&g,2,4,2);
add_edge(&g,4,6,2);
dijkstra(&g,1);
printf("The path from 1 to 8 with cumulative weights:\n");
print_path(&g,8);
delete_graph(&g,8);
return 0;
}
dijkstra.c只对有TODO的部分进行修改(即为void init_graph函数的TODO部分和void dijkstra的TODO部分),具体修改要求详情见代码部分的注释
// DSA Programming task 4.2 - Dijsktra
// You work on this file where TODO is located
#include <stdio.h>
#include <stdlib.h>
#include "dijkstra.h"
// Initializes graph for Dijkstra
void init_graph(weightedgraph* g, int vertices){
g->nVertices = vertices;
int i;
for(i=1; i <= vertices; i++) {
g->adj_list[i] = 0;
g->pred[i] = 0;
// TODO! Note the distance
g->dist[i] = INF;
}
}
// Adds new edge (x,y)
void add_edge(weightedgraph* g, int x, int y, double wght){
if( x <= g->nVertices && y <= g->nVertices){
pweightededgenode pxy = malloc(sizeof(weightededgenode));
pweightededgenode pyx = malloc(sizeof(weightededgenode));
pxy->nodenum = y;
pxy->next = g->adj_list[x];
pxy->weight = wght;
g->adj_list[x] = pxy;
pyx->nodenum = x;
pyx->next = g->adj_list[y];
pyx->weight = wght;
g->adj_list[y] = pyx;
}
}
/*
Dijkstra's algorithm:
DIJKSTRA(G,w,s)
for each vertex v in V
d[v] = INF
p[v] = NIL
d[s] = 0
S = EMPTY
Q = V[G]
while Q != EMPTY
u = EXTRACT-MIN(Q)
S = S UNION {u}
for each vertex v in Adj[u] do
if d[v] > d[u] + w(u,v) then
d[v] = d[u] + w(u,v)
p[v] = u
*/
// Dijkstra search from node s
void dijkstra(weightedgraph* g, int s){
int queue[MAXVERTS];
int i=0;
// Initialize graph
for(i=1; i <= g->nVertices; i++) {
g->pred[i] = 0;
g->dist[i] = INF;
// All vertices in queue
queue[i] = i;
}
// TODO! Modification should start from here
// Note that the propability should be maximized
// Chanage names of variables accordingly
g->dist[s] = 0;
for(i=g->nVertices; i >= 1; i--) {
// Search for minimum from the queue
double minval = g->dist[queue[1]];
int minnode = queue[1];
int minj=1;
for(int j = 1; j <= i; j++) {
if( g->dist[queue[j]] < minval ){
minval = g->dist[queue[j]];
minnode = queue[j];
minj = j;
}
}
// Switches the minimum to end (out of the queue)
int temp = queue[i];
queue[i] = queue[minj];
queue[minj] = temp;
pweightededgenode pedge = g->adj_list[minnode];
// Relax the neighbors
while(pedge != 0){
int v = pedge->nodenum;
if(g->dist[v] > (g->dist[minnode]+pedge->weight)) {
g->dist[v] = g->dist[minnode]+pedge->weight;
g->pred[v] = minnode;
}
pedge = pedge->next;
}
// DEBUG INFO:
// printf("%d processed: d[%d] = %f\n",minnode,minnode,g->dist[minnode]);
}
}
//No need to change anyting after this point!
// Free allocated memory
void delete_graph(weightedgraph* g, int vertices){
int i;
for(i=1; i <= vertices; i++) {
pweightededgenode pedge = g->adj_list[i];
pweightededgenode pnext = 0;
while(pedge != 0) {
pnext = pedge->next;
free(pedge);
pedge = pnext;
}
}
}
// Print a path after search
void print_path(weightedgraph* g, int dest){
if( g->pred[dest] != 0){
print_path(g, g->pred[dest]);
printf("%d:%f\n",dest,g->dist[dest]);
}
else if(g->dist[dest]==0){
printf("%d:%f\n",dest,g->dist[dest]);
}
}
