如何用python求解带有标准正态分布累积分布函数的方程组？

Question

#跪求

• 帮忙解决一个问题，金融专业的大四学生做毕设的时候遇到的
  

  

  
  我在套用布莱克-舒尔斯（B-S）模型的时候出现了这样一个方程组，需要我求出v和sigmav的值，其他的变量都是已知的。可我只在大一的时候学过一点python，就尝试用python解了一下这个方程组。用gekko库我的代码是这么写的：

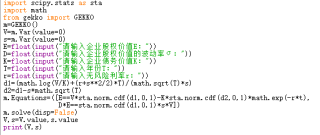
报错，截图如下：

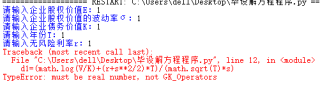
我用sympy库也没有成功，代码和报错的截图如下

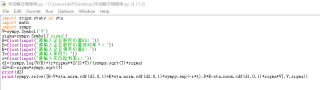
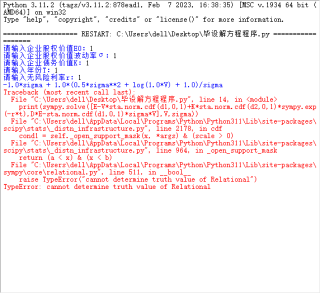
恳请高人伸出援手！

Answer 1

该回答引用于gpt与OKX安生共同编写：

• 该回答引用于gpt与OKX安生共同编写：

你可以使用SciPy库中的optimize.fsolve()函数求解这个方程组，该函数可以对多变量的非线性方程进行求解。以下是一个示例代码：

import numpy as np
from scipy import optimize
from scipy.stats import norm

def f(x, S, K, r, T, C):
    v = x[0]
    sigmav = x[1]
    d1 = (np.log(S/K) + (r + 0.5 * v ** 2) * T) / (sigmav * np.sqrt(T))
    d2 = d1 - sigmav * np.sqrt(T)
    return [S * norm.cdf(d1) - K * np.exp(-r * T) * norm.cdf(d2) - C,
            v - sigmav ** 2 * T]

# 假设已知的参数值
S = 100
K = 105
r = 0.05
T = 0.5
C = 7

# 初始化估计值
x0 = [0.2, 0.3]

# 调用fsolve函数求解方程组
result = optimize.fsolve(f, x0, args=(S, K, r, T, C))

print("v =", result[0])
print("sigmav =", result[1])

在这个代码中，我们首先定义了需要解决的方程组f(x,S,K,r,T,C)，其中x为未知数（即v和sigmav），表达式中涉及到正态分布累积分布函数norm.cdf()来求解方程组。

然后，我们设置了假设已知的参数值，并初始化估计值x0，最后调用optimize.fsolve()函数求解方程组得到最终结果，即v和sigmav的值。

你需要注意的是，这个问题具有多个解，因此初始值x0的设置可能会影响最终结果。如果结果不准确，可以尝试使用不同的初始值进行求解。同时，还需要考虑精度和收敛速度等问题，以便获得更加准确和高效的求解方法。

• 如果不知道估计值，可以考虑使用暴力枚举的方法来求解所有可能的解。

具体步骤如下：

1. 导入需要的库：

import numpy as np
from scipy.stats import norm

1. 定义方程组：

def equations(p):
    v, sigmav = p
    eq1 = 50 - (16*v/np.pi)**0.5 - (1-np.exp(-0.1*10))*(100/(9*np.exp(2*0.1*10)))*norm.cdf((np.log(v/50) + (0.1 + sigmav**2/2)*10)/(sigmav*np.sqrt(10)))
    eq2 = 0.2**2 - ((sigmav**2)*10*v)/(np.pi**2*(1-np.exp(-0.1*10)))
    return [eq1, eq2]

1. 构建一个n维数组，表示 v 和 sigmav 取值范围。然后通过迭代计算每个点的函数值，判断是否满足方程组，如果满足，就把这个点加入到最终结果中。

v_range = np.linspace(0, 100, num=1000)
sigmav_range = np.linspace(0, 100, num=1000)

results = []
for v in v_range:
    for sigmav in sigmav_range:
        # 计算当前点的函数值
        eqs = equations([v, sigmav])
        # 如果方程组的误差小于 1e-6，则将该点的坐标加入到结果列表中
        if abs(eqs[0]) < 1e-6 and abs(eqs[1]) < 1e-6:
            results.append([v, sigmav])

# 输出所有可能的解
for r in results:
    print("v = ", r[0])
    print("sigmav = ", r[1])
    print()

注意：在使用暴力枚举的方法时，需要设置好待求解变量的取值范围和步长（这里使用了np.linspace函数），以免漏解或计算过多无用的点导致程序运行缓慢。