递推与递归之PRG涂色

Question

有排成一行的n个方格，用红(Red)、粉(Pink)、绿(Green)三色涂每个格子，每格涂一色，要求任何相邻的方格不能同色，且首尾两格也不同色．求全部的满足要求的涂法.
输入要求：
输入数据包含多个测试实例,每个测试实例占一行,由一个整数n组成，(0<n<=50)。
输出要求：
对于每个测试实例，请输出全部的满足要求的涂法，每个实例的输出占一行。
样例
    输入：
1
2
输出：
3
6
算法分析：把最后一个和第一格连接在一起，就变成把圆分成几块扇形，进行涂色的问题。
（1）当n = 0, f(n) = 0；n = 1时, 从三种颜色选1种，即f(n) = 3；n = 2时, 从三种颜色选2种排列，即f(n) = 6；n = 3时，从三种颜色选3种排列，即f(n) = 6。
（2）如果有n个方格，当对第n个方格填色时，有两种情况：
①如果已经对前面n-1个方格填好了色，有f(n-1)种情况，此时第n-1个跟第一个颜色一定不一样，所以第n个只有一种选择。则有：f(n-1)
②如果对前面n-2个方格填好色，有f(n-2)种情况，第n-1个空格颜色跟第一个颜色一样，最后第n个方格可以填两种颜色，所以是2*f(n-2);
         综上可以推出：f(n) = f(n-1) + 2*f(n-2), n>=4。
所以，递推公式：

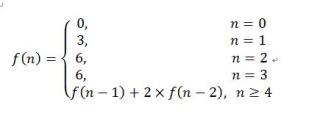
我的代码如下

#include<stdio.h>
int f(int n)
{
    int s;
    if(n==0)
        s=0;
    else if(n==1)
        s=3;
    else if(n==2||n==3)
        s=6;
    else
        s=f(n-1)+2*f(n-2);
    return s;
}
int main()
{
    int n=0,a[100];
    while(scanf("%d",&a[n])!=EOF)
        n++;
    for(int i=0;i<n;i++)
    {
        f(a[i]);
        printf("%d\n",f(a[i]));
    }
    return 0;
}

按照案例数据输入运行结果对可是将代码提交到平台显示

我这个代码该怎么改？求指正

Answer 1

#include<stdio.h>

int f(int n)
{
    int s;
    if(n==0)
        s=0;
    else if(n==1)
        s=3;
    else if(n==2||n==3)
        s=6;
    else
        s=f(n-1)+2*f(n-2);
    return s;
}

int main()
{
    int T, n;
    scanf("%d", &T);
    for(int i = 0; i < T; i++)
    {
        scanf("%d", &n);
        printf("%d\n", f(n));
    }
    return 0;
}