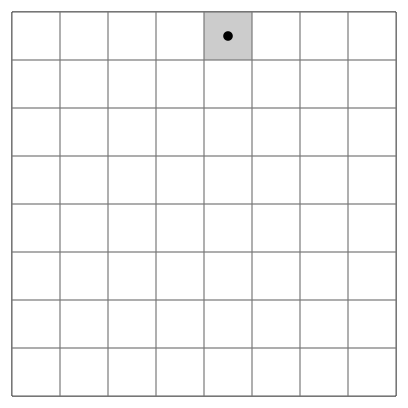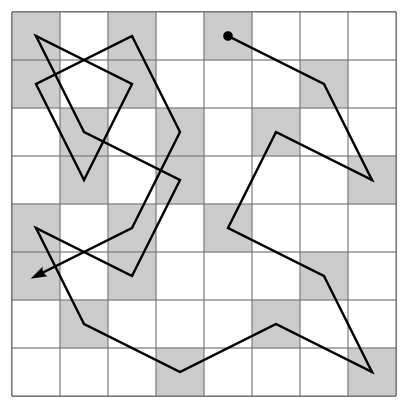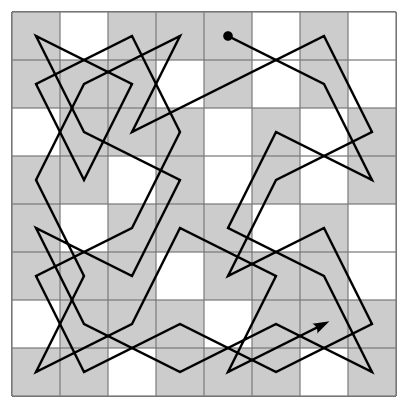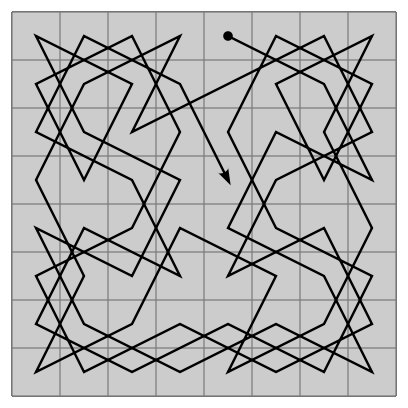
马踏棋盘问题（又称骑士周游或骑士漫游问题）

Question

马踏棋盘问题（又称骑士周游或骑士漫游问题）是算法设计的经典问题之一。

国际象棋的棋盘为8*8的方格棋盘，现将“马”放在任意指定的方格中，按照“马走日”的规则将“马”进行移动，要求每个方格只能进入一次，最终使得“马”走遍棋盘64个方格。
关于国际象棋“马走日”的规则如下：

1 2 3 4 5 6 7 8都是马此刻可以走的位置，马踏棋盘问题的一个实现如下：

请教一下以下代码实现哪个步骤错了？

#include<stdio.h>
int sum = 0;
int PD(int M[8][8],int n,int m);
int PD(int M[8][8],int n,int m)
{
    int i,j;
    
    //判断8个方向的棋点是否能下。 
    if(n-2 >= 0 && m-1 >= 0)
    {
        if(M[n-2][m-1] == 0)
        {
        M[n-2][m-1] = 1;
        PD(M,n-2,m-1);
        }
    }
    
    
    if(n-2 >= 0 && m+1 < 8)
    {
        if(M[n-2][m+1] == 0)
        {
        M[n-2][m+1] = 1;
        PD(M,n-2,m+1);
        }
    }

    if(n-1 >= 0 && m+2 < 8)
    {
        if(M[n-1][m+2] == 0)
        {
        M[n-1][m+2] = 1;
        PD(M,n-1,m+2);
        }
    }
    
    
    if(n+1 < 8 && m+2 < 8)
    {
        if(M[n+1][m+2] == 0)
        {
        M[n+1][m+2] = 1;
        PD(M,n+1,m+2);
        }
    }
    
    if(n+2 < 8 && m+1 < 8)
    {
        if(M[n+2][m+1] == 0)
        {
        M[n+2][m+1] = 1;
        PD(M,n+2,m+1);
        }
    }
    
    if(n+2 < 8 && m-1 >= 0)
    {
        if(M[n+2][m-1] == 0)
        {
        M[n+2][m-1] = 1;
        PD(M,n+2,m-1);
        }
    }
    
    
    if(n+1 < 8 && m-2 >= 0)
    {
        if(M[n+1][m-2] == 0)
        {
        M[n+1][m-2] = 1;
        PD(M,n+1,m-2);
        }
    }
    
    
    if(n-1 >= 0 && m-2 >= 0)
    {
        if(M[n-1][m-2] == 0)
        {
        M[n-1][m-2] = 1;
        PD(M,n-1,m-2);
        }
    }
    
    if(sum == 64)
    {
        printf("%d行%d列\n",n+1,m+1);
        return;
    }
    
    for(i = 0;i < 8; i++)
    {
        for(j = 0;j < 8; j++)
        {
            if(M[i][j] == 1)
            sum++;
        }
    }

    if(sum != 64)
    {
        M[n][m] = 0;
        sum = 0;
        return;
    }

    return 0; 
    
}

int main()
{
    int M[8][8];
    int n,m;

//数组初始化为0  
    for(n = 0;n < 8; n++)
    {
        for(m = 0;m < 8; m++)
        {
        M[n][m] = 0; 
        }
    }

    printf("请选择起始位置 '行 列':");
    scanf("%d %d",&n,&m);
    
    M[n-1][m-1] = 1;
    
    PD(M,n-1,m-1);
    return 0;
}

Answer 1

在该代码实现中，没有判断马是否已经遍历了所有的棋格。在程序中，当sum等于64时，只输出当前所在的行和列，但没有终止程序的执行，因此程序会继续执行，而且在程序中没有添加其他的终止条件，导致程序无限循环。应该在sum等于64时，添加终止程序的代码，例如使用return语句终止程序的执行。另外，也应该将sum的计数重置为0，以便重新计数从当前位置开始能够遍历的棋格数目。