用matlab复现欧拉法求解常微分方程初值问题

Question

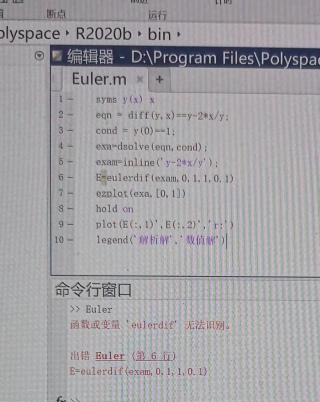
问题：函数或变量'eulerdif'无法识别
按照书上写的，希望有人能帮着解答一下

Answer 1

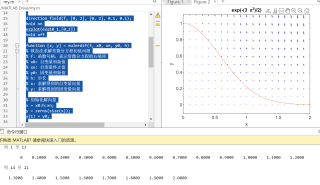
书上的代码只是一部分，不完整，需要自己写函数。我在你代码基础上修改后，增加了自己编写的两个函数，用于计算欧拉法求解，代码如下：

exa10_1=dsolve('Dy=-3* x* y','y(0)=1','x');
exam10_1=inline('-3*x*y');
E=eulerdif(exam10_1,0,2,1,0.1)
ezplot(exa10_1,[0,2])
hold on
plot(E(:,1)',E(:,2)','r:')
legend('解析解','数值解')
hold off
figure
%examp10_1=inline(vectorize('-3* x* y'));
syms x y;
examp10_1 = -3*x*y;
f = matlabFunction(examp10_1);

direction_field(f, [0, 2], [0, 2], 0.1, 0.1);
hold on
ezplot(exa10_1,[0,2])
hold off

function [x, y] = eulerdif(f, x0, xn, y0, h)
% 欧拉法求解常微分方程初值问题
% f: 函数句柄，表示常微分方程的右端项
% x0: 自变量初始值
% xn: 自变量终止值
% y0: 因变量初始值
% h: 步长
% x: 求解得到的自变量向量
% y: 求解得到的因变量向量

% 初始化解向量
x = x0:h:xn;
y = zeros(size(x));
y(1) = y0;

% 使用欧拉法求解
for i = 1:length(x)-1
    y(i+1) = y(i) + h * f(x(i), y(i));
end

end
function direction_field(f, x_range, y_range, x_step, y_step)
% 绘制一阶常微分方程的方向场
% f: 函数句柄，表示一阶常微分方程的右端项
% x_range: 自变量范围
% y_range: 因变量范围
% x_step: 自变量步长
% y_step: 因变量步长

% 创建网格点
[x, y] = meshgrid(x_range(1):x_step:x_range(2), y_range(1):y_step:y_range(2));

% 计算方向场
u = ones(size(x));
v = f(x, y);

% 绘制方向场
quiver(x, y, u, v, 0.5, 'b', 'LineWidth', 1.2);

% 添加坐标轴和标题
xlabel('x');
ylabel('y');
title('Direction Field');

end

运行结果如下：