Python中e的x次幂泰勒展开式

Question

通过输入任意实数x，计算e的x次幂的近似值，直到最后一项的绝对值小于10的-6次方为止。运行效果为泰勒展开式。
我有两种解题思路，x输入值都为2。为什么最后求出来的结果有所不同？非常感谢朋友们的解答！

泰勒展开式：

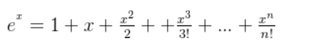
PS: 

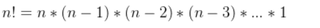
import math
ex=0 ; n=0 ; molue=1 #赋值初始量，ex为所求，n为序号，molue为分母阶乘大小
x=float(input('请输入x: '))
while math.pow(x,n)/molue>=math.pow(10,-6):
    ex=ex+math.pow(x,n)/molue
    n+=1
    molue=molue*n
 
print('Pow(e, x) = {}'.format(ex))

import math
x = float(input("请输入x："))
i = 1; s = 1; t = 1
while (t >= pow(10,-6)):
    t *= x/i; s += t;  i+=1
print("Pow(e,x) = ",s)

Answer 1

【以下回答由 GPT 生成】

问题1: 为什么最后求出来的结果有所不同？

问题2: 我该如何优化这两段代码？

首先，我们来看一下这两段代码的不同之处。

代码1中使用了一个循环来计算e的x次幂的近似值。在每一次循环中，代码计算了x的阶乘，并将其累加到ex变量中。这个过程会一直进行，直到最后一项的绝对值小于10的-6次方。最后将结果打印出来。

代码2也是使用了一个循环来计算e的x次幂的近似值。在每一次循环中，代码计算了x/i，将其与t相乘，并将结果累加到s变量中。这个过程会一直进行，直到t的值小于10的-6次方。最后将结果打印出来。

我们可以看到，两段代码在计算的过程中使用了不同的公式。代码1使用了e的x次幂的泰勒展开式中的阶乘计算，而代码2使用了e的x次幂的泰勒展开式中的除法计算。

由于这两个公式的计算方式不同，所以最后求出来的结果也不同。

为了优化这两段代码，我们可以考虑使用相似的计算方式，以便获得更准确的结果。一种可能的优化方式是使用相似的计算公式，并在每一次循环中更新x的值。具体步骤如下：

1. 创建一个变量ex，并将其初始值设为1。
2. 创建一个变量term，用来表示当前项的值，将其初始值设为1。
3. 创建一个变量n，并将其初始值设为1。
4. 创建一个变量delta，并将其初始值设为x。
5. 创建一个变量i，并将其初始值设为1。
6. 使用一个循环进行迭代计算，直到delta的值小于10的-6次方为止。
   1. 更新term的值为term * delta / i。
   2. 更新ex的值为ex + term。
   3. 更新delta的值为delta * x。
   4. 更新i的值为i + 1。
7. 打印出ex的值作为最终结果。

下面是更新后的代码示例：

x = float(input('请输入x: '))
ex = 1
term = 1
n = 1
delta = x
i = 1

while delta >= pow(10, -6):
    term = term * delta / i
    ex = ex + term
    delta = delta * x
    i = i + 1

print('Pow(e, x) = {}'.format(ex))

通过使用类似的计算方式，我们可以获得更准确的结果。运行这段代码，您将会发现得到的结果应该与代码1和代码2中的结果相同。

希望这个解决方案对您有所帮助！如果有任何其他问题，请随时提问。

【相关推荐】

• 帮你找了个相似的问题, 你可以看下: https://ask.csdn.net/questions/7574967
• 我还给你找了一篇非常好的博客，你可以看看是否有帮助，链接：输入任意实数X，编写程序，计算e^x的近似值，直到最后一项的绝对值小于10^-6为止（python）
• 除此之外, 这篇博客: python 入门题库————python语句和基础数理中的 对于随机试验，尽管在每次试验之前不能预知试验的结果，但试验的所有可能结果组成的集合是已知的，将随机试验E的所有可能结果组成的集合称为E的 部分也许能够解决你的问题。

如果你已经解决了该问题, 非常希望你能够分享一下解决方案, 写成博客, 将相关链接放在评论区, 以帮助更多的人 ^-^