1.请利用回溯算法完成下题的算法设计及时间复杂度分析
物品数量n=3,物品重量w={10,20,30},物品价值p={60,100,120},背包承重m=50。
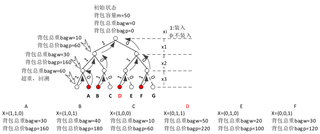
(1)数据结构
背包容量m,物品数量n,物品重量数组w[],物品价值数组p[]。
当前背包重量bagw,当前背包总价bagp,当前最优解x[]
当前最优总价值maxp,最优解maxx[],可用的物品价值r。
(2)迭代公式
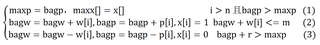
1.请利用回溯算法完成下题的算法设计及时间复杂度分析
物品数量n=3,物品重量w={10,20,30},物品价值p={60,100,120},背包承重m=50。

(1)数据结构
背包容量m,物品数量n,物品重量数组w[],物品价值数组p[]。
当前背包重量bagw,当前背包总价bagp,当前最优解x[]
当前最优总价值maxp,最优解maxx[],可用的物品价值r。
(2)迭代公式
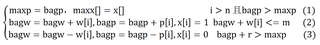
 关注
关注【以下回答由 GPT 生成】
def backtrack(n, w, p, m):
max_value = 0 # 最大总价值
best_items = [] # 最优物品组合
def helper(i, cur_weight, cur_value, cur_items):
nonlocal max_value, best_items
if cur_weight > m:
return
if cur_value > max_value:
max_value = cur_value
best_items = cur_items[:]
if i == n: # 遍历完所有物品
return
# 不选择当前物品
helper(i+1, cur_weight, cur_value, cur_items)
# 选择当前物品
cur_items.append(i)
helper(i+1, cur_weight + w[i], cur_value + p[i], cur_items)
cur_items.pop()
helper(0, 0, 0, [])
return max_value, [w[i] for i in best_items]
n = 3
w = [10, 20, 30]
p = [60, 100, 120]
m = 50
max_value, best_items = backtrack(n, w, p, m)
print("最大总价值:", max_value)
print("物品组合:", best_items)
算法的时间复杂度分析: - 在最坏情况下,对于每一个物品,我们都有两种选择,选择与不选择,所以回溯算法的时间复杂度是O(2^n),其中n是物品的数量。