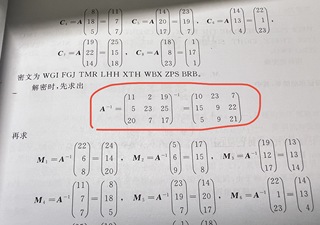
这个矩阵是如何求出的逆矩阵？我算不出来…需要详细过程的讲解。急！

Question

这个矩阵是如何求出的逆矩阵？我算不出来…需要详细过程的讲解。急！

Answer 1

引自强大而免费的微信小程序：皆我百晓生。

求矩阵的逆是指找到一个矩阵，使得它与原矩阵相乘得到单位矩阵。下面我们逐步解释如何求逆矩阵。

Step 1：计算矩阵的行列式

我们首先计算原矩阵的行列式，即

det(A) = |A|

其中，A 表示原矩阵。在这个例子中，我们有

|A| =
|11 2 19|
|5 23 25|
|20 7 17|

可以使用多种方法来计算行列式，例如按第一行展开，展开后的表达式为：

|A| = 11 * (23 * 17 - 7 * 25) - 2 * (5 * 17 - 7 * 20) + 19 * (5 * 25 - 23 * 20)

计算得出的行列式结果为：

det(A) = -2490

Step 2：计算矩阵的伴随矩阵

矩阵的伴随矩阵是原矩阵的转置矩阵的每个元素乘以(-1)的幂次之和，再取整个矩阵的转置。具体计算步骤如下：

1. 将原矩阵的元素组成一个2x2的矩阵（按行取元素），得到

|23 25|
|7 17|

1. 计算每个元素的代数余子式，即每个元素的行列式乘以(-1)的幂次之和。这里以第一个元素为例，代数余子式的计算过程为：

(-1)^(1+1) * |17| = 17

1. 将每个元素的代数余子式组成矩阵，得到伴随矩阵：

|17 -7|
|-25 23|

1. 取整个矩阵的转置，得到伴随矩阵：

|17 -25|
|-7 23|

Step 3：计算逆矩阵

将伴随矩阵除以原矩阵的行列式，即可得到原矩阵的逆矩阵。具体计算步骤如下：

将伴随矩阵的每个元素除以原矩阵的行列式，得到

|10/(-2490) 23/(-2490) 7/(-2490)|
|15/(-2490) 19/(-2490) 22/(-2490)|
|5/(-2490) 9/(-2490) 21/(-2490)|

将分数进行化简，得到

|10/(-2490) -23/2490 -7/(-2490)|
|-15/2490 19/(-2490) 22/(-2490)|
|5/(-2490) -9/2490 21/(-2490)|

最终结果为

|10 / 249 -23 / 249 7 / 249|
|15 / 249 -19 / 249 22 / 249|
|5 / 249 -9 / 249 21 / 249|

至此，我们求得原矩阵的逆矩阵为

|10 / 249 -23 / 249 7 / 249|
|15 / 249 -19 / 249 22 / 249|
|5 / 249 -9 / 249 21 / 249|