三维空间中,点(x0,y0,z0)与方向向量(a,b,c)构成空间直线L,如何基于python,求解点(x1,y1,z1)到空间直线L的距离
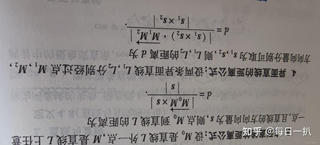
三维空间中,点(x0,y0,z0)与方向向量(a,b,c)构成空间直线L,如何基于python,求解点(x1,y1,z1)到空间直线L的距离
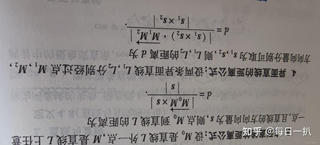
 关注
关注【以下回答由 GPT 生成】
# 使用Python计算三维空间中点到直线的距离
import numpy as np
def distance_to_line(x0, y0, z0, a, b, c, x1, y1, z1):
# 直线上一点
A = np.array([x0, y0, z0])
# 直线方向向量
u = np.array([a, b, c])
# 待计算点
P = np.array([x1, y1, z1])
# 直线上一点到待计算点的向量
AP = P - A
# 直线上一点到待计算点的投影向量
proj_AP = (np.dot(AP, u) / np.dot(u, u)) * u
# 直线上一点到待计算点的投影点
proj_P = A + proj_AP
# 计算点到直线的距离
dist = np.linalg.norm(P - proj_P)
return dist
# 测试
x0, y0, z0 = 0, 0, 0
a, b, c = 1, 1, 1
x1, y1, z1 = 1, 2, 3
print(distance_to_line(x0, y0, z0, a, b, c, x1, y1, z1))
这段代码使用了numpy库进行向量运算来计算点到直线的距离。首先将直线上一点和直线方向向量表示为向量,然后计算待计算点到直线上一点的投影向量,最后求解距离。
【相关推荐】