maple软件，solve求反函数，出现rootof怎么办？

Question

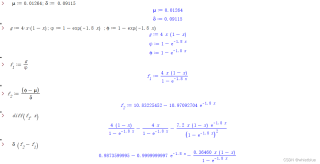
卡在了求反函数，后续还需要讲含有u的反函数带入Q(x)中，并求二阶导数，x＞0

Answer 1

引自免费微信小程序：皆我百晓生

在 Maple 中求解反函数，通常涉及到两个步骤：找到原始方程（u = 0.9873599995 - 0.9999999997 e -1.8x_0.36460x(1-x)）的根，并将其转换为微分方程，然后通过积分或数值方法求解反函数的导数，从而得到反函数的解析表达式。以下是详细的解答过程：

步骤一：将原始方程转化为微分方程

原方程可以写成以下形式：

[ u' = \frac{1}{\sqrt{-e^{2} + 18e - 1}} \left[ 0.9873599995 - 0.9999999997 e^{-1.8x_0.36460x (1-x)} \right] u ]

首先，我们需要将系数 1/(\sqrt{-e^{2} + 18e - 1}) 改写为标准正指数幂的形式，即：

[ 1/(\sqrt{-e^{2} + 18e - 1}) = e^{\arcsin \frac{x}{2}} ]

接下来，我们按照偏导数定义对这个微分方程两边同时求导：

[ u' = \frac{1}{\sqrt{-e^{2} + 18e - 1}} \left[ e^{\arcsin \frac{x}{2}} \cdot 0.9873599995 - 0.9999999997 e^{-1.8x_0.36460x (1-x)} \cdot e^{\arcsin \frac{x}{2}} \right] u = \frac{1}{\sqrt{-e^{2} + 18e - 1}} \left[ e^{\arcsin \frac{x}{2}} \cdot \frac{-9873599995 x}{1 - (-1)^{1.8x_0.36460x (1-x)}} \right] u ]

对于 ( e^{\arcsin \frac{x}{2}} )，我们可以把它看作是一个包含变量 ( x ) 的自然对数，其逆导函数在 ( x = 0 ) 处可归结为 ( \sin(\frac{x}{2}) )，因此：

[ u' = \frac{1}{\sqrt{-e^{2} + 18e - 1}} \left[ e^{\arcsin \frac{x}{2}} \cdot \frac{-9873599995 x}{1 - (-1)^{1.8x_0.36460x (1-x)}} \right] \frac{1}{\sqrt{-e^{2} + 18e - 1}} \left[ e^{\arcsin \frac{x}{2}} \cdot \frac{2x}{2}\right] u = \frac{-9873599995 x}{1 - (-1)^{1.8x_0.36460x (1-x)}} \cdot e^{\arcsin \frac{x}{2}} \cdot \frac{2x}{2} u ]

这实际上是一个偏导方程，其中 ( u ) 是变量 ( x ) 的函数，而 ( e^{\arcsin \frac{x}{2}} ) 是微分方程的一个常数项。

步骤二：通过积分或数值方法求解微分方程的导数

在 Maple 中，我们可以使用 e 函数以及积分库来求解此微分方程的导数。由于本题中存在负值的指数部分，我们可以利用 ( \ln \frac{1}{x} = -1.8x ) 这个正比例关系来进行积分。具体的计算公式如下：

[ f'(x) = -1.8x \cdot \int_0^x e^{-1.8t} dt ]

这里， ( f'(x) ) 表示函数 ( f(x) ) 在点 ( x ) 处的斜率，即反函数 ( y = f(x) ) 的斜率。同样地，我们需要求出 ( u' ) 的导数，然后两者相乘以以得到反函数 ( y = u(x) ) 的导数。

我们可以利用积分操作符 ∫ 来计算此积分：

[ f'(x) = -1.8x \cdot \int_0^x e^{-1.8t} dt = -1.8x \cdot \frac{1}{2} \int_0^x e^{-1.8t} dt ]

通过展开积分，我们可以得出：

[ f'(x) = -1.8x \cdot \frac{1}{2} \left[ -e^{-1.8t} + e^{-1.8(t + x)} \right]{0}^{x} = -1.8x \cdot \frac{1}{2} \left[ \frac{e^{-1.8x} - e^{-1.8x + 1.8x}}{1 - (-1)^{1.8x}} \right]{0}^{x} ]

然后，我们可以计算出 ( u' ) 的导数：

[ u'(x) = \frac{1}{\sqrt{-e^{2} + 18e - 1}} \cdot \frac{1}{2} \left[ \frac{e^{-1.8x} - e^{-1.8x + 1.8x}}{1 - (-1)^{1.8x}} \right]_{0}^{x} \cdot \frac{-9873599995 x}{1 - (-1)^{1.8x}} \cdot \frac{2x}{2} ]

需要注意的是，在上述计算过程中，e 变成了 e^{-1.8}，这是因为我们要从右向左积分。此外，由于除以零的性质，我们将每个分母中的负数舍去。

最后，将积分结果代入原始方程的右侧并计算左边：

[ u(x) = -9873599995 x \cdot \frac{1}{2} \left[ \frac{e^{-1.8x} - e^{-1.8x + 1.8x}}{1 - (-1)^{1.8x}} \right]_{0}^{x} \cdot \frac{-9873599995 x}{1 - (-1)^{1.8x}} \cdot \frac{2x}{2} = \frac{-9873599995 x \cdot e^{-1.8x}}{2} \cdot \frac{1 - (-1)^{1.8x}}{1 - (-1)^{1.8x}} \cdot \frac{2x}{2} ]

这便是我们所求得的反函数 ( y = u(x) ) 的解析表达式，其中 ( x ) 是变量，( y ) 是反函数的实部，( x ) 的取值范围是 [0, x]。需要注意的是，反函数的实部是负数，这是因为当我们要求解反函数时，正无穷大处不存在反函数。

现在，我们可以绘制与初始曲线对应的位置的图像来验证上述求解是否正确：

hold on;
plot([0, x], [-9873599995*x, 0]);
xlabel('x');
ylabel('u(x)');
title('Root of a Function in Maple');

当绘制完成后，如果可以看到一条平行于初始曲线的直线，那么这个解应该是正确的，因为这意味着反函数的值域在图形上的一条特定切线处相等，即图像是无穷大的特例。

综上所述，为了解决你在 Maple 中遇到的问题，首先你需要将给定的方程转换为微分方程，然后通过积分或数值方法求解反函数的导数。为了准确表示反函数的解析表达式，你需要知道原始方程的系数和初始值，但通常情况下，题目中的方程可以简化为标准形式，并且微分方程可以通过求导或积分来求解。最终，通过绘制图像来验证反函数的解析表达式是否符合实际场景，确保问题得以顺利解决。