求解四个变换矩阵中的未知数θ

Question

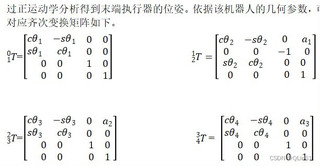
通过逆矩阵，用矩阵中已知参数表示未知参数，未知参数分别是四个θ的值

Answer 1

以下内容由CHATGPT及阿里嘎多学长共同生成、有用望采纳：

---

根据您提供的图片内容，我们可以看到两个文件包含了一系列与机器人运动学相关的矩阵方程。这些矩阵方程涉及到了正运动学问题，其中未知数θ代表机器人关节的角度。在正运动学中，我们通常从已知的关节角度计算末端执行器的位置和姿态。

首先，我们需要明确一点，逆矩阵通常用于求解线性方程组，而正运动学问题通常涉及到非线性方程组。因此，直接使用逆矩阵来求解θ的值可能不是最直接的方法。不过，我们可以通过建立方程组并使用非线性求解器来解决这个问题。

以下是使用MATLAB求解未知数θ的一般步骤：

1. 建立方程组：根据给定的变换矩阵，将方程中的已知参数和未知参数θ表示出来。

2. 定义目标函数：由于正运动学问题是非线性的，我们需要定义一个目标函数，该函数计算当前θ值下预测的变换矩阵与实际变换矩阵之间的差异。

3. 使用非线性求解器：MATLAB提供了多种非线性求解器，如fsolve或lsqnonlin，可以用来求解方程组中的未知数θ。

4. 迭代求解：使用非线性求解器进行迭代，直到找到满足精度要求的θ值。

5. 验证结果：求解完成后，需要验证得到的θ值是否合理，可以通过将这些值代入原方程来检查。

由于您提供的图片中没有具体的数值，我无法给出具体的MATLAB代码。但是，我可以提供一个大致的MATLAB代码框架，您可以根据实际情况进行调整：

% 假设已知的变换矩阵和参数
T1 = [...]; % 第一个变换矩阵
T2 = [...]; % 第二个变换矩阵
T3 = [...]; % 第三个变换矩阵
T4 = [...]; % 第四个变换矩阵

% 定义目标函数，计算预测矩阵与实际矩阵的差异
function F = objective(theta)
    theta1 = theta(1);
    theta2 = theta(2);
    theta3 = theta(3);
    theta4 = theta(4);
    
    % 根据theta计算预测的变换矩阵
    T1_pred = ...; % 根据theta1计算预测的T1
    T2_pred = ...; % 根据theta2计算预测的T2
    T3_pred = ...; % 根据theta3计算预测的T3
    T4_pred = ...; % 根据theta4计算预测的T4
    
    % 计算误差
    F(1) = norm(T1 - T1_pred);
    F(2) = norm(T2 - T2_pred);
    F(3) = norm(T3 - T3_pred);
    F(4) = norm(T4 - T4_pred);
end

% 初始猜测值
theta0 = [0, 0, 0, 0];

% 使用非线性求解器求解
options = optimoptions('fsolve', 'Display', 'iter');
theta_solution = fsolve(@objective, theta0, options);

% 输出结果
disp('Solution for theta:');
disp(theta_solution);

请注意，您需要根据具体的变换矩阵和已知参数来填充T1_pred, T2_pred, T3_pred, T4_pred的计算部分，以及初始化theta0。

如果您需要进一步的帮助来解决这个问题，或者需要具体的数值来测试代码，请提供更多的信息。