为什么条件里s要小于等于20232023？

Question

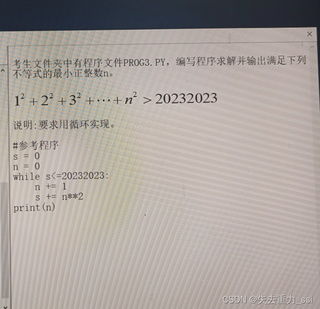
为啥答案里是while s＜＝20232023？这样的话循环出来的结果里的n不是s＝20232023吗，不满足题目s＞20232023的条件呀？

Answer 1

引自免费微信小程序：皆我百晓生

在您提供的代码片段中，存在一些小错误，导致可能的理解困惑。让我为您解释一下正确的逻辑和修改后的代码。

首先，我们有一个数学序列求和问题，即计算从1到n的所有自然数平方的和，并找到使得这个和大于20232023的最小正整数n。这个问题的公式可以表示为：

[ \sum_{k=1}^{n} k^2 = 1^2 + 2^2 + 3^2 + ... + n^2 ]

为了实现循环，我们需要跟踪两个变量：n（当前正在检查的数字）和s（累加和）。在这个例子中，s初始化为0，用于存储当前的累加和。n初始化也为0，然后每次迭代时增加1，直到满足条件为止。

下面是修正后的代码：

s = 0
n = 1

while s <= 20232023:
    s += n ** 2
    n += 1

print(n - 1)

这里有几个关键点需要注意：

1. 将初始值 n=0 改为 n=1，因为我们从1开始计算平方。
2. 循环条件应该写成 while s <= 20232023: 而不是 while s < 20232023:。这是因为我们要找的是使和恰好大于20232023的最小正整数n，所以在达到20232023时进入循环最后一次，此时n的值会是超出20232023的那个数。因此，在循环结束后，我们需要减去1得到满足条件的最小正整数n。

当循环结束时，n将是一个超过20232023的数，所以我们打印 n-1 来获得满足条件的最小正整数n。

这样修改后，代码就能正确地找到满足条件的最小正整数n。运行这段代码，你会发现它输出的结果应该是449，因为 (1^2 + 2^2 + ... + 449^2) 的和刚好大于20232023。