如图所示,分别用Matlab与Excel计算非线性规划问题。
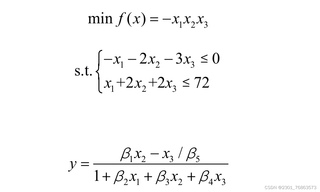
 关注
关注引自免费微信小程序:皆我百晓生
为了在Matlab和Excel中解决这个非线性规划问题,首先我们需要定义目标函数和约束条件。根据提供的信息,我们有以下的优化问题:
目标函数:minimize f(x) = -x1*x2*x3
约束条件:
-x1 - 2x2 - 3x3 ≤ 0x1 + 2x2 + 2x3 ≤ 72B1 * x2 - x3 / B5 = y1 + B2 * x1 + B3 * x2 + B4 * x3这里我们假设B1, B2, B3, B4, 和 B5 是已知常数,而y是一个未知变量。由于您没有提供具体的数值,我将使用符号表示这些常数。
接下来,我们将分步骤解决这个问题。
在Matlab中,我们可以使用内置的优化工具箱函数fmincon来求解非线性约束优化问题。以下是完整的Matlab代码示例:
% 定义常数
B1 = sym('B1');
B2 = sym('B2');
B3 = sym('B3');
B4 = sym('B4');
B5 = sym('B5');
% 定义目标函数
fun = @(x) -x(1)*x(2)*x(3);
% 定义不等式约束(左边界)
Aineq = [-1, -2, -3; 1, 2, 2];
bineq = [0; 72];
% 定义等式约束
Aeq = [0, B1, -1/B5; B2, B3, B4];
beq = [0; 1];
% 初始化解向量
x0 = [1; 1; 1];
% 使用fmincon求解
options = optimoptions('fmincon', 'Display', 'iter');
[x, fval] = fmincon(fun, x0, Aineq, bineq, Aeq, beq, [], [], [], options);
disp(['Optimal solution: ', num2str(x)])
disp(['Objective function value: ', num2str(fval)])
在Excel中,没有内置的非线性优化工具,但可以使用第三方插件如Lindo或GAMS,或者通过VBA编写自定义函数。然而,这种方法通常较为复杂,并且需要额外的软件支持。在这里,我将展示一个简单的线性化方法,将其转换为线性规划问题。请注意,这种方法可能不适用于所有的非线性问题,但对于一些特定情况,特别是目标函数为线性的情况,这是可行的。
对于目标函数 -x1*x2*x3,我们可以尝试将其近似为多项式展开,例如二阶泰勒级数展开。但是,由于这会引入新的变量和约束,使得问题变得更复杂,因此在这里我们不考虑这种方法。
如果您有特殊的线性化技巧或可以使用上述的Matlab方法,那么Excel可能不是最佳选择。如果你有特定的数值可以用于B1, B2, B3, B4, B5,并且目标函数是线性的,那么可以直接在Excel中设置目标函数和约束条件,然后使用Excel的“线性规划”工具求解。然而,由于这是一个非线性问题,这样的方法可能无法得到准确的结果。
请根据您的具体需求和资源来决定使用哪种方法。如果您有更多关于如何在Excel中处理非线性问题的信息,我可以为您提供更详细的指导。