matlab可以把相图转换为庞加莱映射吗

Question

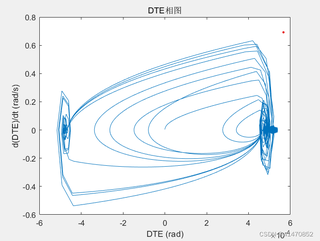
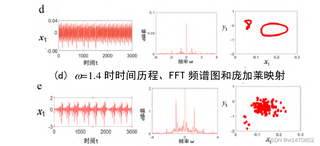
主程序见图二图三,求解微分方程,目前已得出微分方程的时域响应以及相图,可否再把相图转换为如下图所示的庞加莱映射,有合适的修改建议吗,感谢感谢

clear;clc;close all;
%初始参数，该参数变化，myfun程序要对应调整
syms t;
syms v;
% t=@(v)(505.2*ln(49897/(55000-398.7*v))+1460*(12.8-v)/398.7);
v=@(t)finverse(t);  
t_of_v = @(v)(505.2*log(49897/(55000-398.7*v))*2.3+1460*(12.8-v)/398.7);
% % 使用数值方法求解速度 v 关于时间 t 的反函数
finverse = @(t) fzero(@(v) t_of_v(v)-t, 5);
zi=4;%内转子极对数
zo=14;%外转子极对数k
z1=32;%小齿轮齿数
z2=99;%大齿轮齿数
ms=4.62e-3;
I=z2/z1;%机械齿轮速比
G=(zo+zi)/zi;%磁齿轮速比
%一、计算过程
tmax=4.79;
tspan = 0:1e-4:tmax;
bc=1e-4;
y0=[0;0;0;wm_func(0);wm_func(0)/G;wm_func(0)/(G*I)];
[t,y]=odeRK4sys('myfun3',tmax,bc,y0);

figure;plot(t,y(:,1)/G-y(:,2));
signal = y(:,1)/G - y(:,2);
set(gca,'FontSize',16);
title('时域响应图','FontSize',16);
xlabel('时间 (s)','FontSize',16);
ylabel('扭转振幅(rad)','FontSize',16);%磁齿轮的相对弹性角度
figure;plot(t,y(:,2)/I-y(:,3));
signal1=y(:,2)/I-y(:,3);
set(gca,'FontSize',16);
title('时域响应图','FontSize',16);
xlabel('时间 (s)','FontSize',16);
ylabel('扭转振幅(rad)','FontSize',16);%机械齿轮的相对弹性转角;

DTE = y(:,1)/G - y(:,2); % DTE (电磁弹性角度)
dDTE_dt = gradient(DTE, t); % DTE的一阶导数
% 绘制相图
figure;
plot(DTE, dDTE_dt);
title('DTE相图');
xlabel('DTE (rad)');
ylabel('d(DTE)/dt (rad/s)');
DTE = y(:,2)/I - y(:,3); % DTE (电磁弹性角度)
dDTE_dt = gradient(DTE, t); % DTE的一阶导数
% 绘制相图
figure;
plot(DTE, dDTE_dt);
title('DTE相图');
xlabel('DTE (rad)');
ylabel('d(DTE)/dt (rad/s)');

function dydt=myfun3(t,y,wm_func)
v=@(t)finverse(t);  
t_of_v = @(v)(505.2*log(49897/(55000-398.7*v))*2.3+1460*(12.8-v)/398.7);
finverse = @(t) fzero(@(v) t_of_v(v)-t, 5);
wm_func = @(t)((finverse(t)*3.6)*9550/(3600*0.4064/(0.93*14)))*pi*2/60;
wm=wm_func(t);
zi=4;%内转子极对数
zo=14;%外转子极对数
z1=32;%小齿轮齿数
z2=99;%大齿轮齿数
arf0=20/180*pi;%压力角
ms=4.62e-3;
r2=ms*z1/2;%小齿轮分度圆
r3=ms*z2/2;%大齿轮分度圆
rb2=r2*cos(arf0);%小齿轮基圆
rb3=r3*cos(arf0);%大齿轮基圆
I=z2/z1;%机械齿轮速比
G=(zo+zi)/zi;%磁齿轮速比

Tm=9550*55/(60*wm/(2*pi));  
% Tm=114.8;
TL=Tm*I*G;%变速器负载
%3 转动惯量
IM=0.081197;%电机转子转动惯量kgm2
I0=0.181197;%磁齿轮低速级转动惯量kgm2
I1=0.013663;%磁齿轮高速级转动惯量kgm2
I2=0.0230596;%机械小齿轮转动惯量
I3=1.9825692;%机械大齿轮转动惯量
IL=21;%整车等效转动惯量

%4 刚度与阻尼
%齿轮的阻尼和刚度
w1=wm*G;%机械小齿轮输入转速
kp=10.51e8;
kb=0.25e8;%两个齿轮的刚度曲线为正弦曲线，
km=kp+kb*sin(w1*t*z1);
sg=0.16;%齿轮阻尼比
cm=2*sg*sqrt(kp*I2*I3/(I2*rb3^2+I3*rb2^2));

 b=1e-4;
 xx=rb2*y(2)-rb3*y(3);
 dxx=rb2*y(5)-rb3*y(6);

  if xx-b>0
      fx=xx-b;
  elseif xx+b<0
      fx=xx+b;
  else
      fx=0;
  end
F23=km*fx+cm*dxx;
T0=1.7*Tm*G;
Tc1=0.2*T0*sin(wm*t);
Tc=0.1*(zi*y(4)-(zi+zo)*y(5));
T21=T0*sin(zi*y(1)-(zi+zo)*y(2))+Tc+Tc1;
y(7)=(Tm-T21/G)/(I0+IM);
y(8)=(T21-r2*F23)/(I2+I1);
y(9)=(-TL+r3*F23)/(I3+IL);
dydt=[y(4)
      y(5)
      y(6)
      y(7)
      y(8)
      y(9)];
end

Answer 1

引自免费微信小程序：皆我百晓生

在MATLAB中，你可以将相图转换为庞加莱映射图。庞加莱映射是一种在相平面上展示系统动态行为的方法，特别是在非线性振荡器和混沌系统中。庞加莱映射图通常在时间历程分析中使用，可以显示系统的周期性行为或混沌行为。为了生成庞加莱映射图，你需要在相图上对每个周期或者特定的时间间隔取点，并在一个二维图中绘制这些点。以下是一个可能的步骤和代码示例：

首先，你需要确定系统的周期或采样间隔。然后，在相图上对每个时间点的状态进行采样，得到一系列的（DTE, dDTE_dt）对。接着，把这些点绘制在同一图上即可得到庞加莱映射。以下是一个简单的代码示例：

假设你已经得到了系统的时域响应和相图，你可以使用如下代码来生成庞加莱映射：

% 已有时域响应数据 y 和对应的时间 t
% 假设 y(:,1) 是 DTE 的时域响应，y(:,2) 是 dDTE_dt 的时域响应
% 确定系统的周期或采样间隔
sampling_interval = 0.01; % 例如每0.01秒采样一次

% 初始化庞加莱映射的坐标数组
pMap_DTE = []; % 用于存储庞加莱映射中的 DTE 值
pMap_ddTE_dt = []; % 用于存储庞加莱映射中的 dDTE_dt 值

% 计算庞加莱映射
for i = 1:length(t) - 1
    if mod(i, 1/sampling_interval) == 0 % 确保按照设定的间隔采样点
        pMap_DTE = [pMap_DTE; y(:, 1)(i)]; % 添加当前点的 DTE 值到庞加莱映射数组
        pMap_ddTE_dt = [pMap_ddTE_dt; y(:, 2)(i)]; % 添加当前点的 dDTE_dt 值到庞加莱映射数组
    end
end

% 绘制庞加莱映射图
figure; plot(pMap_DTE, pMap_ddTE_dt, 'o'); % 'o' 表示数据点用圆圈标记出来
title('庞加莱映射图'); xlabel('DTE (rad)'); ylabel('d(DTE)/dt (rad/s)');

这段代码将根据设定的采样间隔对相图上的点进行采样，并绘制出庞加莱映射图。需要注意的是，你需要根据实际情况调整采样间隔以及确认相图中的变量对应关系。另外，你可能需要根据你的系统和具体应用情况进一步调整和完善代码。如果你的系统有特定的周期性或混沌行为，可能需要更复杂的采样策略来捕捉这些行为。