matlab求解指数函数方程组

Question

使用matlab代码解下面方程组

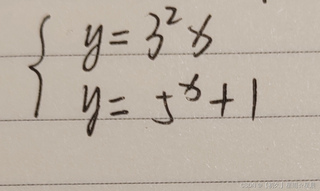
希望附有每个步骤的详细注释和相关语法解释

Answer 1

该回答引用自GPT-3.5, 由博主 GISer Liu 编写：

好的，下面是一个详细的解决方案，用于在MATLAB中求解指数函数方程组。我们将逐步解释每个步骤，并附上详细的注释和语法解释。

问题描述

假设我们有以下指数函数方程组：
[ \begin{cases}
a \cdot e^{bx} = y_1 \
a \cdot e^{bx} = y_2
\end{cases} ]
其中 (a) 和 (b) 是未知数，(x) 和 (y_1, y_2) 是已知数。

解决方案

1. 定义已知数和方程组
2. 使用符号变量
3. 构建方程组
4. 求解方程组

详细步骤和代码

% 步骤1：定义已知数
x = [1, 2]; % 已知x值
y = [2.718, 7.389]; % 已知y值

% 步骤2：使用符号变量
syms a b; % 定义符号变量a和b

% 步骤3：构建方程组
eqn1 = a * exp(b * x(1)) == y(1); % 第一个方程
eqn2 = a * exp(b * x(2)) == y(2); % 第二个方程

% 步骤4：求解方程组
sol = solve([eqn1, eqn2], [a, b]); % 求解方程组

% 步骤5：提取解
a_sol = double(sol.a); % 将符号解转换为数值
b_sol = double(sol.b); % 将符号解转换为数值

% 输出结果
fprintf('a = %.4f\n', a_sol);
fprintf('b = %.4f\n', b_sol);

详细注释和语法解释

1. 定义已知数

   x = [1, 2]; % 已知x值
   y = [2.718, 7.389]; % 已知y值
   

   这里我们定义了已知的 (x) 和 (y) 值。

2. 使用符号变量

   syms a b; % 定义符号变量a和b
   

   使用 syms 命令定义符号变量 (a) 和 (b)。

3. 构建方程组

   eqn1 = a * exp(b * x(1)) == y(1); % 第一个方程
   eqn2 = a * exp(b * x(2)) == y(2); % 第二个方程
   

   使用符号变量构建方程组。exp 函数用于计算指数函数。

4. 求解方程组

   sol = solve([eqn1, eqn2], [a, b]); % 求解方程组
   

   使用 solve 函数求解方程组。第一个参数是方程组，第二个参数是未知数。

5. 提取解

   a_sol = double(sol.a); % 将符号解转换为数值
   b_sol = double(sol.b); % 将符号解转换为数值
   

   使用 double 函数将符号解转换为数值解。

6. 输出结果

   fprintf('a = %.4f\n', a_sol);
   fprintf('b = %.4f\n', b_sol);
   

   使用 fprintf 函数输出结果，保留四位小数。

总结

通过上述步骤和代码，我们可以在MATLAB中求解指数函数方程组，并得到 (a) 和 (b) 的数值解。每个步骤都有详细的注释和语法解释，确保用户可以理解和复现整个过程。

如果该回答解决了您的问题，请采纳！如果没有，请私信联系或评论您的疑惑