矩阵的向量化和向量的矩阵化

Question

矩阵的向量化和kronecker积有关，如下图，向量的矩阵化呢？

Answer 1

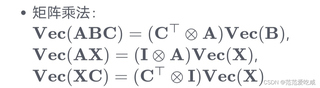
以下回复参考：皆我百晓生、券券喵儿等免费微信小程序作答:

矩阵的向量化(Vec)操作是将矩阵的元素重新排列成一个长向量。对于两个矩阵$A$和$B$的乘积$C = AB$，其向量化表示为：

$$\text{Vec}(C) = (B^T \otimes A)\text{Vec}(B)$$

其中$\otimes$表示Kronecker积，它是一种特殊的矩阵乘法，用于将两个矩阵合并成一个新的更大的矩阵。在这个公式中，$B^T$是矩阵$B$的转置，而$\text{Vec}(B)$是将矩阵$B$向量化的结果。

对于矩阵$A$和向量$X$的乘积$Y = AX$，其向量化表示为：

$$\text{Vec}(Y) = (I_A \otimes X)\text{Vec}(A)$$

其中$I_A$是一个与矩阵$A$同阶数的单位矩阵。

对于向量$X$和矩阵$C$的乘积$Z = XC$，其向量化表示为：

$$\text{Vec}(Z) = (C^T \otimes I_X)\text{Vec}(X)$$

其中$I_X$是一个与向量$X$同阶数的单位矩阵。

向量的矩阵化是将一个长向量重新排列成一个矩阵的过程。这通常是向量化操作的逆过程。例如，如果有一个向量$\text{v}$，它是由矩阵$M$向量化得到的，那么可以通过矩阵化操作将$\text{v}$恢复为矩阵$M$。

在图1和图2中，似乎有一些重复的内容，可能是由于格式错误或者复制粘贴时的错误。正确的表达应该是上述的向量化公式。