一道密码学LFSR的题，要解答过程和答案

Question

一个4级LFSR的结构常数是=(1, 0, 1, 1)。
（1）请画出此LFSR的结构图，给出反馈函数；

（2）若初始状态为1101，求输出序列和周期。

Answer 1

(1) LFSR 结构图与反馈函数
对于给定的4级线性反馈移位寄存器（LFSR），其结构常数为(1, 0, 1, 1)，这意味着第4个位置（最左边）的输出与第2个和第3个位置的输出进行异或运算后，作为新输入值反馈回第1个位置（最右边）。这里的位置编号从右到左依次增加。

反馈函数
如果我们将LFSR的四个位置分别标记为
Q3, Q2, Q1 和 Q0，那么反馈函数可以表示为:
F(Q3,Q2,Q1,Q0)=Q3⊕Q2⊕Q0 其中⊕表示异或操作。
结构图

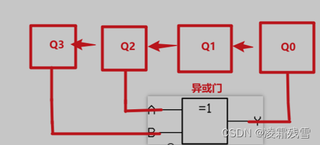
(2) 输出序列和周期
给定初始状态为1101，我们可以手动计算几个步骤来找到输出序列及其周期。

初始状态: 1101
第1步: 1⊕0⊕1=01⊕0⊕1=0, 新状态: 1100
第2步: 1⊕0⊕0=11⊕0⊕0=1, 新状态: 1101
第3步: 1⊕0⊕1=01⊕0⊕1=0, 新状态: 1110
第4步: 1⊕1⊕0=01⊕1⊕0=0, 新状态: 1110
第5步: 1⊕1⊕0=01⊕1⊕0=0, 新状态: 1111
第6步: 1⊕1⊕1=11⊕1⊕1=1, 新状态: 1111
第7步: 1⊕1⊕1=11⊕1⊕1=1, 新状态: 1111
第8步: 1⊕1⊕1=11⊕1⊕1=1, 新状态: 0111
第9步: 0⊕1⊕1=00⊕1⊕1=0, 新状态: 1011
第10步: 1⊕0⊕1=01⊕0⊕1=0, 新状态: 1101
从上述步骤可以看出，当状态再次变为1101时，我们已经完成了一个完整的循环。因此，输出序列为11011110，并且周期为15（包括所有可能的状态，除了全0状态，因为全0状态会导致LFSR陷入停滞）。

请注意，实际上，对于一个4级LFSR，最大可能的周期是
2的4次幂−1=15,因为我们排除了全0状态，该状态不会产生任何有意义的输出。在这个例子中，我们确实达到了最大周期15，这表明给定的反馈多项式是本原的，能够产生最长的非重复序列。