DFS算法优化python

Question

洛谷上的题目：

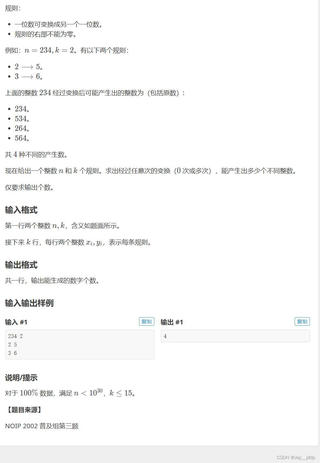
这是我的代码，应该是当n很大时，超时以及超内存了，要怎么修改我的代码啊，用的是python

def dfs(rule,n,total_number):
    if n in total_number:
        return
    total_number.add(n)
    for i in range(len(n)):
        flag = int(n[i])
        if flag in rule:
            new_flag = rule[flag]
            new_n = n[:i] + str(new_flag) + n[i+1:]
            dfs(rule,new_n,total_number)

def count_number(rule,n,k):
    n = str(n)
    total_number = set()    #存储可能产生的数（不重复）
    dfs(rule,n,total_number)
    return len(total_number)
    

if __name__ == '__main__':
    n,k = map(int,input().split())
    rule = {}
    for i in range(k):
        x,y = map(int,input().split())
        rule[x] = y
    print(count_number(rule,n,k))

Answer 1

以下回复参考：皆我百晓生、券券喵儿等免费微信小程序作答:

你的代码使用深度优先搜索（DFS）来生成所有可能的数字，这是一个很好的思路。然而，当数字n非常大时，可能的组合数量也会非常大，导致你的代码运行时间过长。在这种情况下，优化你的代码的主要方向是减少重复计算和避免不必要的搜索。

以下是一些优化建议：

1. 避免重复计算：在你的代码中，每次递归调用dfs函数时，都会将当前的数字n转换为字符串。如果n非常大，这个操作会消耗大量的时间和内存。你可以将n转换为字符串的操作只在一个地方进行，然后在整个搜索过程中使用字符串的副本。
2. 使用集合来存储规则：在你的代码中，每次查找规则时，你都在整个规则字典中搜索。你可以将规则存储在一个集合中，这样查找规则的时间复杂度就会从O(k)降低到O(1)。
3. 避免不必要的搜索：在你的代码中，你搜索了所有可能的数字组合，包括那些只包含规则转换的数字的组合。然而，题目只要求输出不同整数的数量，所以你可以避免搜索这些组合。例如，如果规则是2→5和3→6，那么数字"23"和"53"应该被认为是相同的组合。你可以使用一个额外的集合来跟踪已经生成的数字的前缀，以避免不必要的搜索。

下面是优化后的代码示例：

def count_number(rules, n, k):
    n_str = str(n)  # 将n转换为字符串，只在这个地方进行转换
    total_numbers = set()  # 存储可能产生的数字（不重复）
    rule_mapping = set(rules)  # 将规则存储为集合以提高查找效率
    generated_prefixes = set()  # 存储已经生成的数字前缀

    def dfs(num_prefix):
        if num_prefix in generated_prefixes:  # 避免重复生成相同的数字前缀
            return
        generated_prefixes.add(num_prefix)  # 添加新的前缀到已生成的列表中
        if len(num_prefix) == len(n_str):  # 如果已经生成了完整的数字，添加到总数中
            total_numbers.add(num_prefix)
        else:  # 继续生成后续的数字
            last_digit = int(num_prefix[-1])  # 获取当前数字的最后一个数字
            if last_digit in rule_mapping:  # 如果存在规则转换
                new_digit = rules[last_digit]  # 获取新的数字
                dfs(num_prefix + str(new_digit))  # 递归生成新的数字前缀
                if new_digit != 0:  # 避免生成以零结尾的数字（不符合规则）
                    dfs(num_prefix[:-1] + str(new_digit))  # 删除最后一个数字并添加新的数字进行递归搜索
    
    dfs('')  # 从空字符串开始搜索所有可能的组合
    return len(total_numbers)  # 返回生成的数字总数

if __name__ == '__main__':
    n, k = map(int, input().split())
    rules = {}  # 存储规则映射的字典，键为原始数字，值为新的数字
    for _ in range(k):
        x, y = map(int, input().split())
        rules[x] = y  # 添加规则到字典中
    print(count_number(rules, n, k))  # 输出生成的数字总数

这些优化应该能够显著提高你的代码的性能，特别是对于较大的输入值。